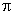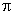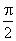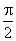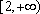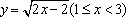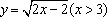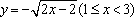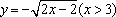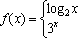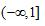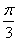- 函数的概念与基本初等函数
- 共5812题
定义在







正确答案
0
解析
略
知识点
如果函数y


正确答案
解析
略
知识点
已知函数
(1)若函数



(2)求函数
(3)若函数


正确答案
见解析
解析
(1)解:
由已知

(2)解:函数

1)当



2)当

当

由上表可知,函数

单调递增区间是
(3)解:由

由已知函数

则

即

即

令


所以


所以
知识点
已知函数






正确答案
解析
略
知识点
已知



正确答案
解析
知识点
已知向量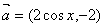
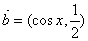
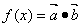
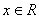
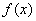
正确答案
解析
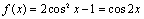
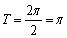
知识点
下列函数中,既是偶函数又在
正确答案
解析
略
知识点
设a为常数,函数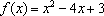
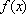
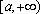

正确答案
解析
略
知识点
函数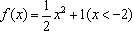
正确答案
解析
略
知识点
已知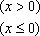
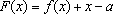

正确答案
解析
略
知识点
已知函数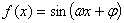
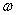
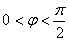
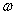
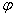
正确答案
2,
解析
略
知识点
对于定义域为










(1)判断函数
(2)证明:
(3)是否存在正整数


正确答案
见解析
解析
(1)是N上的严格增函数.
此因由于






(2)证明:对
由已知

(3)若


设

由



由③有


依此类推可知
且存在

函数值正好从
又因为




所以存在
知识点
设函数f(x)=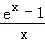
(1)判断函数f(x)在(0,+∞)上的单调性;
(2)证明:对任意正数a,存在正数x,使不等式|f(x)﹣1|<a成立。
正确答案
见解析。
解析
解:(1)f′(x)=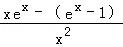
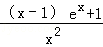
令h(x)=(x﹣1)ex+1,则h′(x)=ex+ex(x﹣1)=xex,
当x>0时,h′(x)=xex>0,∴h(x)是上的增函数,
∴h(x)>h(0)=0
故f′(x)=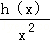
(2)|f(x)﹣1|=|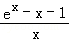
当x>0时,令g(x)=ex﹣x﹣1,则g′(x)=ex﹣1>0
故g(x)>g(0)=0,∴|f(x)﹣1|=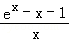
原不等式化为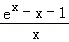
令∅(x)=ex﹣(1+a)x﹣1,则∅′(x)=ex﹣(1+a),
由∅(x)=0得:ex=1+a,解得x=ln(1+a),
当0<x<ln(1+a)时,∅′(x)<0;当x>ln(1+a)时,∅′(x)>0。
故当x=ln(1+a)时,∅(x)取最小值∅[ln(1+a)]=a﹣(1+a)ln(1+a),
令s(a)=
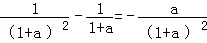
故s(a)<a(0)=0,即∅[ln(1+a)]=a﹣(1+a)ln(1+a)<0。
因此,存在正数x=ln(1+a),使原不等式成立。
知识点
已知函数



(1)用n表示

(2)求:
(3)设

试比较

正确答案
见解析。
解析
(1)
∴函数

令

∵数列


(2)
(3)∵




∴对于正整数n,当

当
知识点
已知函数
(1)当

(2)若


(3)设

正确答案
见解析。
解析
(1)当
令

当

∴当

(2)证明:
又
即对

(3)解法一:函数

将方程
由(1)知
令
则



∴当


当



解法二:
当


则当



当



∴函数
当

∴函数
综上可知,当

当


知识点
扫码查看完整答案与解析