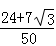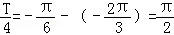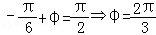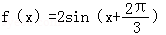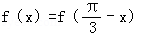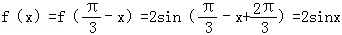- 函数的概念与基本初等函数
- 共5812题
15.若函数

正确答案
2
解析
略
知识点
14. 设函数f(x)=
正确答案
x≤8
解析
略
知识点
7.函数f(x)=x+sinx(x∈R)( )
正确答案
解析
∵f(x)=x+sinx,∴f(﹣x)=﹣x﹣sinx=﹣f(x),则函数f(x)是奇函数.函数的导数f′(x)=1+cosx≥0,则函数f(x)单调递增,为增函数.故选:D
知识点
8. 若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是( )
正确答案
解析
略
知识点
19. 设a∈[-2,0],已知函数
(1)证明f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(2)设曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,且x1x2x3≠0.证明x1+x2+x3>
正确答案
见解析
解析
证明:(1)设函数f1(x)=x3-(a+5)x(x≤0),f2(x)=
①f1′(x)=3x2-(a+5),由a∈[-2,0],
从而当-1<x<0时,f1′(x)=3x2-(a+5)<3-a-5≤0,所以函数f1(x)在区间(-1,0]内单调递减.
②f2′(x)=3x2-(a+3)x+a=(3x-a)(x-1),由于a∈[-2,0],所以当0<x<1时,f2′(x)<0;当x>1时,f2′(x)>0.即函数f2(x)在区间[0,1)内单调递减,在区间(1,+∞)内单调递增.
综合①,②及f1(0)=f2(0),可知函数f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增.
(2)由(1)知f′(x)在区间(-∞,0)内单调递减,在区间

因为曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,
从而x1,x2,x3互不相等,
且f′(x1)=f′(x2)=f′(x3).不妨设x1<0<x2<x3,
由


可得


设g(x)=3x2-(a+3)x+a,则
由

所以x1+x2+x3>
设t=

因为a∈[-2,0],所以t∈
故x1+x2+x3>

知识点
14.若不存在实数x使|x﹣3|+|x+1|≤a成立,则实数a的取值范围是________。
正确答案
(-∞,4)
解析
略。
知识点
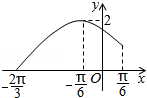
18.定义在区间[﹣
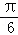
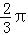

(1)求函数y=f(x)的表达式;
(2)设θ∈[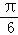
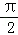

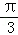
正确答案
(1)f(x)=
(2)
解析
(1)当 x∈[﹣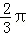
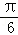
∴T=2π,故ω=1
又f(x)=Asin(ωx+φ)过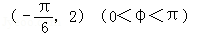
∴
∴
∵函数y=f (x)的图象关于直线
∴
当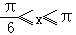
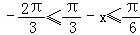
∴
∴f(x)=
(2)∵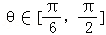
∴由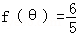
因此,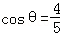
∴
=
知识点
4.将函数y=sin(2x﹣

正确答案
解析
将函数y=sin(2x﹣



知识点
21.已知函数f(x)=2lnx+
(1)当函数f(x)在点(1,f(1))处的切线与直线y﹣4x+1=0垂直时,求实数m的值;
(2)若x≥1时,f(x)≥1恒成立,求实数m的取值范围.
正确答案
见解析。
解析
(1)∵f′(x)=

∴函数f(x)在点(1,f(1))处的切线的斜率k=f′(1)=2﹣
∵函数f(x)在点(1,f(1))处的切线与直线y﹣4x+1=0垂直,
∴2﹣

(2)依题意不等式2lnx+


∴x≥1时,g′(x)<0,∴函数g(x)在[1,+∞)时为减函数,∴g(x)≤g(1)=2,∴m≥2
即实数m的取值范围是[2,+∞).
知识点
21.已知函数f(x)=x2﹣mlnx,h(x)=x2﹣ax+1(a>0)
(1)设A是函数f(x)=x2﹣mlnx上的定点,且f(x)在A点的切线与y轴垂直,求m的值;
(2)讨论f(x)的单调性;
(3)若存在实数m使函数f(x),h(x)在公共定义域上具有相同的单调性,求证:m≥﹣
正确答案
见解析。
解析
(1)由题意得:A(1,1),
又f′(x)=2x﹣
∵f(x)在A点的切线与y轴垂直,
∴f′(1)=0,∴2﹣m=0,∴m=2;
(2)∵f′(x)=2x﹣

∴若m≤0则f(x)在(0,+∞)单调递增,
若m>0,由f′(x)>0,可得x>

由f′(x)<0可得0<x<
∴m>0时,f(x)的递增区间是(

综上可得:m≤0时,f(x)增区间为(0,+∞),无减区间,
m>0时,f(x)的递增区间是(

(3)易知f(x),h(x)的公共定域为(0,+∞),
∵在(0,+∞)上,h(x)的递增区间是(

∴若存在实数m使函数f(x),h(x)在公共定域上具有相同的单调性,
再由(2)可得m=0且


令g(a)=m+

则g(a)=


∴g′(a)=a2+a﹣6,(a>0),
由g′(a)>0,解得:a<﹣3,(舍),或a>2,
由g′(a)<0,解得:0<a<2,
∴g(a)在(0,2)递减,在(2,+∞)递增;
∴g(a)min=f(2)=

∴g(a)≥g(2)=0,即m≥﹣
知识点
4.已知




正确答案
解析
结合图像,由奇函数性质易得答案。选B
知识点
11.定义域为R的偶函数f(x)满足∀x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18.若函数y=f(x)﹣loga(x+1)至少有三个零点,则a的取值范围是( )
正确答案
解析
∵f(x+2)=f(x)﹣f(1),且f(x)是定义域
为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),
f(﹣1)=f(1),
即 f(1)=0 则有,f(x+2)=f(x),
∴f(x)是周期为2的偶函数.
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2,
函数的图象为开口向下.顶点为(3,0)的抛物线.
∵函数y=f(x)﹣loga(|x|+1)在(0,+∞)上
至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至少有3个交点.
∵f(x)≤0,∴g(x)≤0,可得a<1.
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
则有g(2)>f(2),可得 loga(2+1)>f(2)=﹣2,
∴loga3>﹣2,∴3<


又a>0,∴0<a<
故选:B.
知识点
5.设随机变量

正确答案
解析
因为
所以P(2<X<4)= 
知识点
8.已知函数

正确答案
解析
∵f(x)=

∴f(﹣x)=1﹣
∴f(x)+f(﹣x)=2;
∵f(a)=
∴f(﹣a)=2﹣f(a)=2﹣

故选C.
知识点
17.已知函数

(1)求函数
(2)已知







正确答案
见解析。
解析
(1)

由




(2)∵

∵


即
由余弦定理

即
∴
知识点
扫码查看完整答案与解析