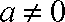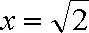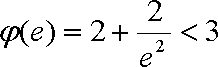- 函数的概念与基本初等函数
- 共5812题
10.若定义在区间








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知某运动物体的位移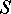
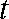
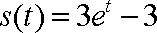
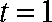
正确答案
3e
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数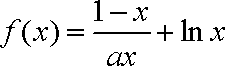
(1)讨论函数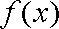
(2)若对任意
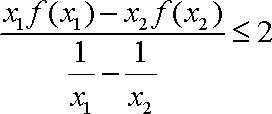
正确答案
见解析。
解析
(1)由已知函数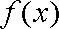
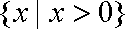

① 
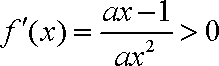
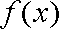
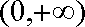
② 
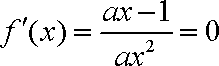
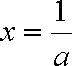
当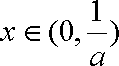
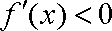

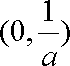
当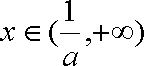
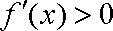
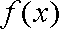
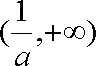
(2)由已知
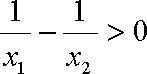
则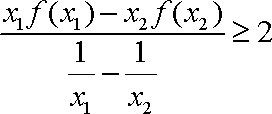
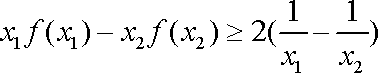
即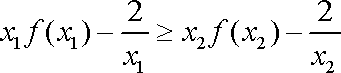
设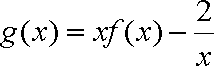

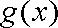
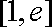
而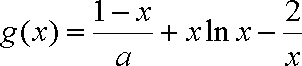
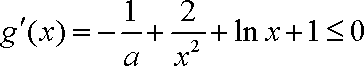
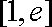
进而转化为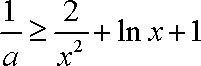
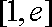
又设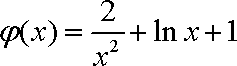
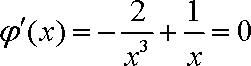
当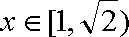
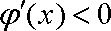
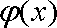
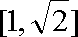
当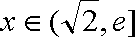
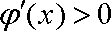

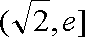
∴当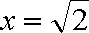

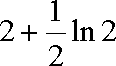
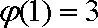
从而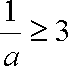
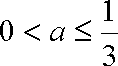
知识点
12.已知函数





正确答案
解析
若a=0则方程f(f(x))=0有无数个实根,不满足条件,
若a≠0,若f(f(x))=0,则f(x)=1,∵x>0时,f(
关于x的方程f(f(x))=0有且只有一个实数解,
故当x≤0时,a•ex=1无解,即ex=
故

知识点
18.如图

















(1)若



(2)求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


(1)求

(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)求函数
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列图形中可以表示以M={x|0≤x≤1}为定义域,以N={y|0≤y≤1}为值域的函数的图象是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如果点P在平面区域


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数






(1)判断函数
(2)若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知





(1)记函数


(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给出定义:若






①


②点

③函数
④ 函数

则其中真命题是______.
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析