- 函数的概念与基本初等函数
- 共5812题
17.已知函数
(1)求
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.下列说法,正确的是( )
正确答案
解析
函数





























知识点
10.设












正确答案
解析
令
















知识点
6.函数
正确答案
解析







知识点
12.△ABC的内角A、B、C的对边分别为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某学校参加数学竞赛学生成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求参加数学竞赛人数n及分数在

(2)若要从分数在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
自变量





知识点
13.已知函数

①图象

②图象

③函数

④由


其中正确的说法的序号为____________。
正确答案
②③
解析







当



将函数



综上所述,正确的命题序号是②③.
知识点
14.已知函数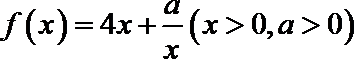
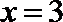
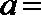
正确答案
解析
当
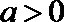
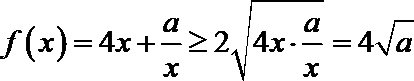
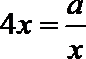


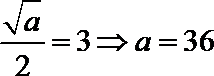
知识点
18.设函数


终边经过点
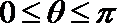
(1)若点
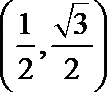

(2)若点
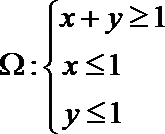
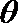

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下面给出的四个点中,到直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.将正整数12分解成两个正整数的乘积有









①
②
③
④
其中正确的序号为_______(填入所有正确的序号).
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
8.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.把函数

则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析














































