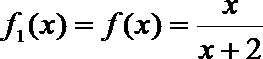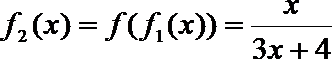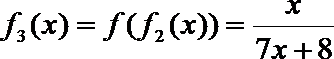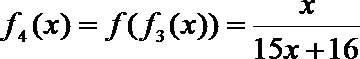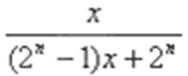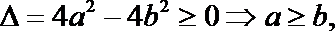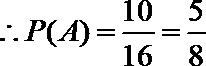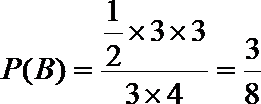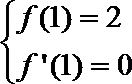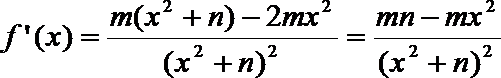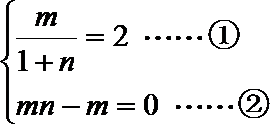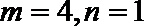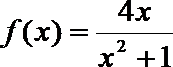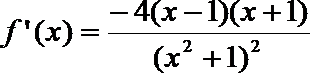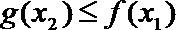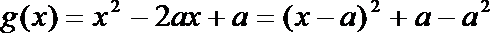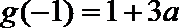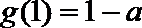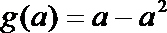- 函数的概念与基本初等函数
- 共5812题
16.





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
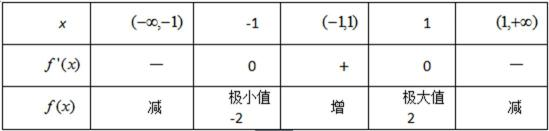
20.设二次函数



(1)求函数
(2)若对于任意的


正确答案
(1)设
∵ 

∴
(2)
∴
即
解析
解析已在路上飞奔,马上就到!
知识点
10.如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数

(1)若

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 函数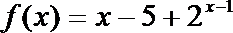
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数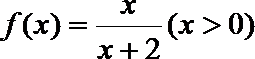
……
依此类推,归纳推理可得当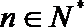
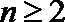
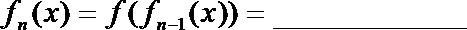
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设关于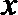
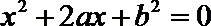
(1)若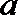
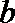
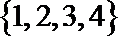
(2)若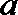
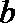
正确答案
(1)设事件A=“方程有实根”,记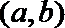
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
一共16种且每种情况被取到的可能性相同
∵关于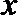
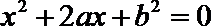
∴
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(4,4)共10种
∴方程有实根的概率是
(2)设事件B=“方程有实根”,记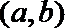
∵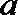
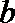
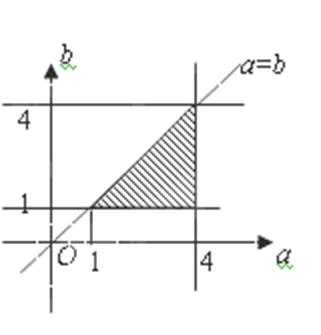
∴点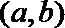
又满足: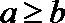
∴
∴方程有实根的概率是
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数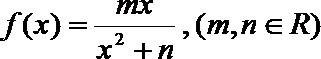
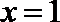
(1)求函数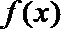
(2)求函数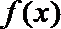
(3)设函数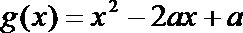
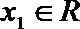
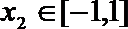
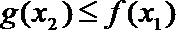

正确答案
(1)∵函数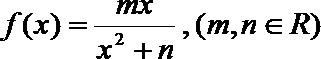
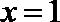
∴
又
∴
由②式得m=0或n=1,但m=0显然不合题意
∴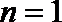
∴
经检验,当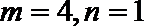
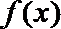
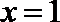
∴函数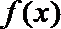
(2)∵函数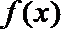
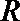
令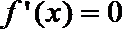
∴当x变化时,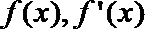
∴当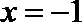
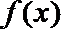
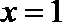
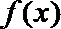
(3)依题意只需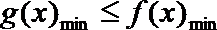
∵函数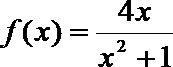
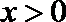
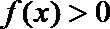
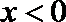
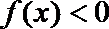
∴ 由(2)知函数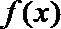
∴当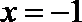
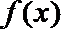
又对任意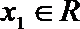
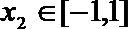
∴当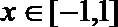
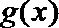
又
①当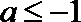
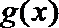
∴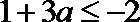
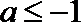
②当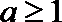
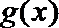
∴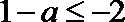
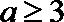
③当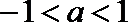
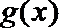
∴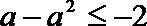
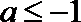
又∵
∴此时a不存在
综上所述,a的取值范围是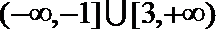
解析
解析已在路上飞奔,马上就到!
知识点
11.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.对于函数








(1)判断函数
(2)已知







(3)在(2)的条件下,令

正确答案
(1)
∴
∴ 是“幅度函数”,其“幅度”为2
(2)
∵ 


∴ 当
当
∴ 
∴
(3)
令

∴
解析
解析已在路上飞奔,马上就到!
知识点
4.下列函数中,既是奇函数又是增函数的是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.(1)m为何值时,f(x)=x2+2mx+3m+4.有且仅有一个零点;
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围。
正确答案
(1)f(x)=x2+2mx+3m+4有且仅有一个零点⇔方程f(x)=0有两个相等实根
⇔Δ=0,
即4m2-4(3m+4)=0,即m2-3m-4=0,
∴m=4或m=-1.
(2)令f(x)=0,得|4x-x2|+a=0,即|4x-x2|=-a.
令g(x)=|4x-x2|, h(x)=-a.
作出g(x)、h(x)的图象.
由图象可知,当0<-a<4,
即-4<a<0时,g(x)与h(x)的图象有4个交点,即f(x)有4个零点.
故a的取值范围为(-4,0).
解析
解析已在路上飞奔,马上就到!
知识点
15.若对任意










(1)非负性:

(2)对称性:
(3)三角形不等式:
今给出个二元函数:
①
②
③
④
则能够成为关于的


正确答案
①
解析
解析已在路上飞奔,马上就到!
知识点
5.为了得到

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析