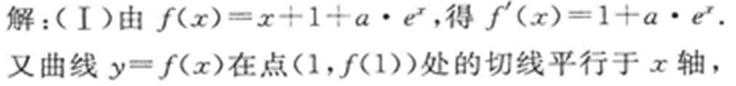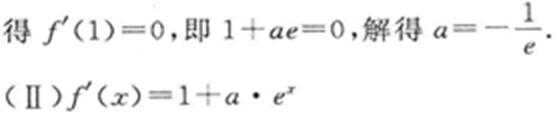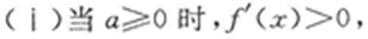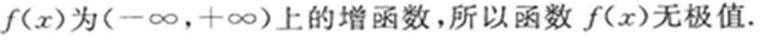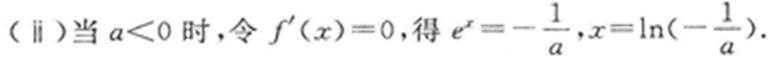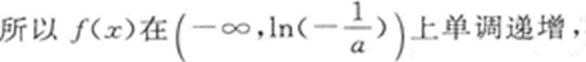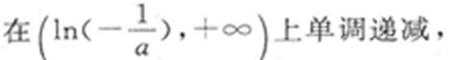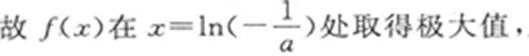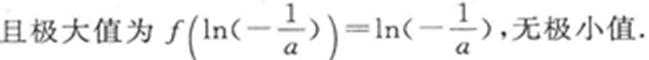- 函数的概念与基本初等函数
- 共5812题
15．已知函数f（x）=
（Ⅰ）求ω的值；
（Ⅱ）在△ABC中，a，b，c分别是角A、B、C的对边，且f（A）=2，求角A的大小及
正确答案
（Ⅰ）f（x）=
∵函数图象上两相邻最高点的坐标分别为（
∴函数的周期T=
则ω=2；
（Ⅱ）∵f（A）=2sin（2A﹣
∴sin（2A﹣
∵0＜A＜π，
∴﹣
∴2A﹣
由正弦定理得：
∵0＜C＜
∴0＜
∴
解析
解析已在路上飞奔，马上就到！
知识点
3．函数
A
B
C
D
正确答案
解析
令
知识点
11．已知命题
正确答案
解析
因为命题
又因为“
知识点
17．某工厂有一批货物由海上从甲地运往乙地，已知轮船的最大航行速度为60海里/小时，甲地至乙地之间的海上航行距离为600海里，每小时的运输成本由燃料费和其它费用组成，轮船每小时的燃料费与轮船速度的平方成正比，比例系数为0．5，其它费用为每小时1250元．
（1）请把全程运输成本
（2）为使全程运输成本最小，轮船应以多大速度行驶？
正确答案
（1）
（2）50．
解析
（1） 由题意得：
即：
（2）由（1）知，
当
因此，函数
在
故为使全程运输成本最小，
轮船应以
知识点
10．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．下列函数在定义域内为奇函数的是（ ）
A
B
C
D
正确答案
解析
由奇函数的定义可知：
知识点
15．已知函数
（1）求函数
（2）若对
（3）
正确答案
（1）极大值是
（2）
（3）
解析
（1）
解得
因此函数的极大值是
（2）因为
所以
因此由（1）可知：
函数
所以
由（2）得：
函数
所以
知识点
16．已知函数
（1）求函数
（2）求函数
正确答案
（1）
（2）
解析
（1）
令
解得
（2）由 
得
函数
知识点
19．已知函数
（1）判断
（2）求函数
（3）令
正确答案
（1）单调递增;
（2）2；
（3）
解析
（1）设
所以
（2）由（1）知：
所以
又
显然
所以
因为
所以
（3）设
则
不妨设
由于
解得
知识点
4．已知
A
B2
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．某工厂引入一条生产线，投入资金250万元，每生产x千件，需另投入成本
（I）写出年利润
（II）年产量为多少千件时该厂的利润最大．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2． 函数f（x）=sin（x+
A（
B（0，1）
C（0，0）
D（- 
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8． 在股票买卖过程中，经常用到两种曲线，一种是即时价格曲线y=f（x），一种是平均价格曲线y=g（x）（如f（2）=3表示开始交易后第2小时的即时价格为3元；g（2）=4表示开始交易后两个小时内所有成交股票的平均价格为4元）．下面所给出的四个图象中，实线表示y=f（x），虚线表示y=g（x），其中可能正确的是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10． 
正确答案
8
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数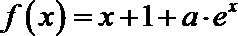
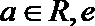
（I）若曲线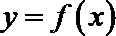
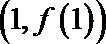
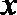
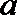
（II）求函数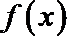
（III）当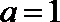
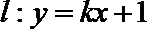
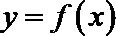
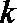
正确答案
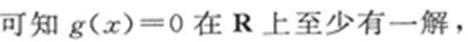
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析