- 函数的概念与基本初等函数
- 共5812题
14.如图,





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数


正确答案
-18
解析
解析已在路上飞奔,马上就到!
知识点
12.已知







正确答案
70
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数



(1)若




(2)求

(3)试探究能否存在区间







正确答案
(1)
(2)
(3)
②若

在


在


由于






综上,当

使得


当




解析
解析已在路上飞奔,马上就到!
知识点
2.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知两座灯塔A.B与C的距离都是a,灯塔A在C的北偏东20°,灯塔B在C的南偏东40°,则灯塔A与灯塔B的距离为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数f(x)=cos 
(1)求函数f(x)的最大值和最小正周期;
(2)设A、B、C为△ABC的三个内角,若cosB=

正确答案
(1)
所以函数f(x)的最大值为
(2)


因为C为锐角,所以C=
在△ABC中,cosB=
所以sinA=sin(B+C)=sinBcosC+cosBsinC
解析
解析已在路上飞奔,马上就到!
知识点
19.某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观察点A.B两地相距100m,∠BAC=60°,在A地听到弹射声音的时间比B地晚
正确答案
由题意,设|AC|=x,
则|BC|=x-
在△ABC内,由余弦定理:
|BC|2=|BA|2+|CA|2-2|BA|·|CA|·cos∠BAC,
即(x-40)2=x2+10000-100x,
解得x=420.
在△ACH中,|AC|=420,
∠CAH=30°+15°=45°,
∠CHA=90°-30°=60°,
由正弦定理:
可得
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求不等式
(2)设


正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)求函数
(2)在区间



正确答案
(1)函数

当
即

当
即

所以,


(2)由不等式

令
由题意可转化为:
在区间


令
由表可知:


所以
因此,所求

解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数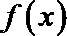
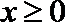
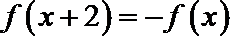
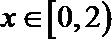
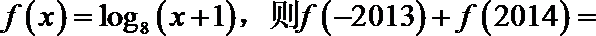
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ< 
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x-

正确答案
(1)由题设图象知,
周期T=2(


因为点(
所以Asin(2×
即sin(
又因为0<φ<
所以
从而

又点(0,1)在函数图象上,
所以Asin
故函数f(x)的解析式为f(x)=2sin(2x+
(2)g(x)=2sin[2(x-



=2sin2x-2sin(2x+
=2sin2x-2(

=sin2x-

由2kπ-


得kπ-

所以函数g(x)的单调递增区间是[kπ-

解析
解析已在路上飞奔,马上就到!
知识点
7.变量x,y满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析

































































