- 函数的概念与基本初等函数
- 共5812题
20.定义在D上的函数






(1)当




(2)若函数

正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
3.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x),一种是平均价格曲线y=g(x) ,( 如f(2)=3表示开始交易后第2小时的即时价格为3元;g(2)=4表示开始交易后两个小时内所有成交股票的平均价格为4元 ).下面所给出的四个图象中,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.定义一个对应法则












正确答案

解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数f(x)=2sinxcosx+cos2x.
(Ⅰ)求f (
(Ⅱ)设




正确答案
(Ⅰ)∵f(x)=sin2x+cos2x,
∴f(


(Ⅱ)∵f(

∴1+sin2α=

∴ cos2α=

∴2α∈(π,
故cos2α=
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数f(x)=2sin x cos x-
(1)求f(x)的最小正周期;
(2)当x∈
正确答案
(1)T=
(2)最大3最小2
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(Ⅰ)若函数

(Ⅱ)设函数
(Ⅲ)设
正确答案
略
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知函数
(Ⅰ)求实数
(Ⅱ)若方程

(Ⅲ)对于(2)中的函数

正确答案
(Ⅰ)


由
因为当

所以

(Ⅱ)由下表:
画出
依题意得:
解得:
所以函数

(Ⅲ)对任意的实数

依题意有:函数


在区间





所以


解析
解析已在路上飞奔,马上就到!
知识点
6.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.抛掷两枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数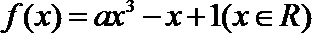


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析