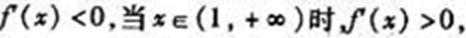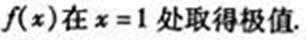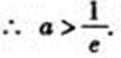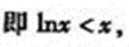- 函数的概念与基本初等函数
- 共5812题
15.过点A(3,1)的直线


正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数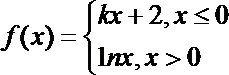
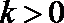
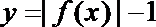
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知三角形的一边长为4,所对角为60°,则另两边长之积的最大值等于____________。
正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
16.设命题p:函数


正确答案
p:
q:
∵“p且q”为假命题 ∴p,q至少有一假
(1)若p真q假,则
(2)若p假q真,则
(3)若p假q假,则
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(I)求函数
(II)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设m,n是两条不同直线,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.经市场调查,某旅游城市在过去的一个月内(以






(1)求该城市的旅游日收益

(2)求该城市旅游日收益的最小值。
正确答案
(1)
(2)当


当

所以


所以

解析
解析已在路上飞奔,马上就到!
知识点
21.函数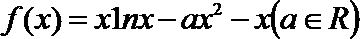
(I)若函数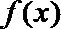
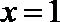
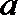
(II)若函数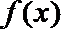
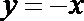
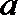
(III)求证: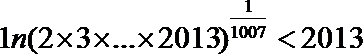
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在直四棱柱


(1)求证:
(2)设




正确答案
(1)连接


(2)取


解析
解析已在路上飞奔,马上就到!
知识点
12.某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如右图所示.根据此频率分布直方图,可知重量超过500克的产品共有________件.
正确答案
26
解析
解析已在路上飞奔,马上就到!
知识点
18. 设

(Ⅰ)若函数


(Ⅱ)当

正确答案
(Ⅰ)
(Ⅱ)答案略。
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.对于数集







(Ⅰ)若

(Ⅱ)若X具有性质P,求证:1X,且当

(Ⅲ)若X具有性质P,且


正确答案
(Ⅰ)选取

所以x=2b,从而x=4.
(Ⅱ)证明:取


由



因为-1是X中唯一的负数,所以

故1
假设


选取



则



若
若

所以x1=1.
(Ⅲ)[答案法一]猜测
记
先证明:若

任取






当



因为




从而


假设








现用数学归纳法证明:
当n=2时,结论显然成立;
假设n=k时,

当n=k+1时,若
也有性质P,所以
取



若
所以



综上所述,
[答案法二]设



记
原点对称.
注意到-1是X中的唯一负数,
所以
由于
……
注意到


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析