- 函数的概念与基本初等函数
- 共5812题
14.若二次函数


正确答案
c
解析
解析已在路上飞奔,马上就到!
知识点
2.若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.为了解某地高三学生的身体发育情况,抽查该地区100名年龄在17.5-18岁之间的男生体重(kg)得到频率分布直方图如下:
根据上图可得这100名学生中体重在[56.5,64.5]的学生人数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数y=cos2x﹣sin2x的最小正周期为_________.
正确答案
π
解析
解:y=
=
=
∴ 最小正周期为
故答案为π.
知识点
4.若函数f(x)=x2+|x+2a﹣1|+a的图象关于y轴对称,则实数a=_________.
正确答案
解析
∵ 函数f(x)=x2+|x+2a﹣1|+a的图象关于y轴对称,
∴ f(x)=f(﹣x),
即x2+|x+2a﹣1|+a=x2+|﹣x+2a﹣1|+a,
|x+2a﹣1|=|x﹣2a+1|,
2a﹣1=0
a=
知识点
10.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若二次函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)若



(2)对于任意的实数





(3)在(1)的条件下,设


正确答案
(1)
(2)
(3)
同理可得:
综上述:
解析
解析已在路上飞奔,马上就到!
知识点
10.

正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
3.函数y=x2﹣1(x<﹣1)的反函数是_________.
正确答案
y=﹣
解析
解:由y=x2﹣1(x<﹣1),
解得
把x与y互换可得y=﹣
∴ 函数y=x2﹣1(x<﹣1)的反函数是y=﹣
故答案为:y=﹣
知识点
7.偶函数f(x)在[0,+∞)上单调递增,且f(3)=0,若f(2x﹣1)<0,则实数x的取值范围是_________.
正确答案
(-1,2)
解析
∵ 偶函数f(x)在[0,+∞)上单调递增,且f(3)=0,
∴ f(2x﹣1)<0可化为
﹣3<2x﹣1<3,
解得﹣1<x<2,
故答案为:(﹣1,2).
知识点
11.设函数f(x)=x2+loga(bx+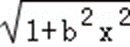
正确答案
3.3
解析
∵ f(x)=x2+loga(bx+
∴ f(2)=4+loga(2b+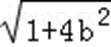
解得loga(2b+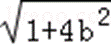
∴ f(﹣2)=4+loga(﹣2b+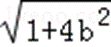
=4﹣loga(2b+
=4﹣0.7
=3.3.
知识点
12.已知AB=2,∠B=60°,AC=b,若b∈M时△ABC能唯一确定,则集合M=_________.
正确答案
解析
∵ △ABC中,∠ABC=60°,AC=b,AB=2,
∴ 由正弦定理





∵ 0 °<C<120°,∴0<sinC≤1,
且b≥2,
则b的取值范围为M=[2,+∞)∪ {
知识点
14.若定义在R上的函数f(x)是奇函数,f(x﹣2)是偶函数,且当0<x≤2时,f(x)=
正确答案
24
解析
∵ 定义在R上的函数f(x)是奇函数,
∴ f(﹣x)=﹣f(x),
∵ f(x﹣2)是偶函数,
∴ f(x﹣2)=f(﹣x﹣2),
f(2﹣x)=f(2+x),
即f(x)=f(4﹣x),
f(x+4)=﹣f(x),
∴ f(x+8)=f(x),
可得周期为8,x=2为对称轴,
∵ f(x)=f(3),
∴ x1=1,x2=3,x3=9,x4=11,x5=17,x6=19,
∵ 在区间(0,16)上的所有实数根之和,
∴ x1+x2+x3+x4=1+3+9+11=24,
知识点
10.已知f(x)是定义在[﹣2,2]上的函数,对于任意实数x1,x2∈[﹣2,2],且x1≠x2时,恒有,
正确答案
4
解析
∵ f(x)是定义在[﹣2,2]上的函数,
对于任意实数x1,x2∈[﹣2,2],且x1≠x2时,
恒有,
∴ f(x)在[﹣2,2]上是单调递增数,
∵ f(x)的最大值为1,
∴ f(2)=1
∵ f(log2x)=1,
∴ log2x=2,x=4
知识点
扫码查看完整答案与解析


















