- 函数的概念与基本初等函数
- 共5812题
19.设函数sgn(x)=
正确答案
解:①当lnx>0,即x>1时,
f(x)=sgn(lnx)﹣ln2x=0可化为:1﹣ln2x=0,
解得,x=e;
②当lnx=0,即x=1时,
f(x)=sgn(lnx)﹣ln2x=0可化为0﹣ln21=0,显然成立;
③当lnx<0,即0<x<1时,
f(x)=sgn(lnx)﹣ln2x=0可化为:
﹣1﹣ln2x=0,
无解;
综上所述,
x=e或x=1.
解析
解析已在路上飞奔,马上就到!
知识点
21.定义:若对任意x1、x2∈(a,b)恒有f(



(1)试判断y=x2是否为R上的凹函数,并说明理由;
(2)若x、y、z∈R,且x+y+2z=8,试求x2+y2+2z2的最小值并指出取得最小值时x、y、z的值.
正确答案
解:(1)f(





∴ 对任意x1、x2∈(a,b)恒有f(

∴ y=x2是R上的凹函数;
(2)∵(x2+y2+2z2)(12+12+
∴ x2+y2+2z2≥16,当且仅当x=y=
∵ x+y+2z=8,∴ x=y=4(

∴ x2+y2+2z2的最小值为16,
此时x=y=4(

解析
解析已在路上飞奔,马上就到!
知识点
5. 函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(Ⅰ)求
(Ⅱ)求
正确答案
解:(I)
∴


(II)原式
解析
解析已在路上飞奔,马上就到!
知识点
21.已知


(Ⅰ)求

(Ⅱ)求
(Ⅲ)当



正确答案
解:(I)







(II)解:由(1)知
由于




由上表知:当




(III)由已知,得

即:

令





即:

解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数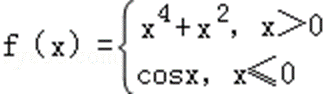
正确答案
解析
选项A,
∵ 函数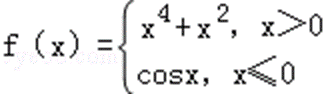
∴ f(1)=14+12=2,
f(﹣1)=cos(﹣1)=cos1≠2.
∴ f(﹣x)=f(x).
∴ f(x)不是偶函数;
选项B,
当x=﹣2π时,f(﹣2π)=cos(﹣2π)=1,
当x=﹣π时,f(﹣π)=cos(﹣π)=﹣1,
∵ ﹣2π<﹣π,f(﹣2π>f(﹣π),
∴ f(x)在(﹣∞,+∞)上不是增函数;
选项C,
∵ f(x)在(0,+∞)是增函数;
∴ f(x)不是周期函数;
选项D,
当x>0时,y=x4+x2>0,
当x≤0时,y=cosx∈[﹣1,1],
∴ f(x)的值域为[﹣1,+∞).
故选D.
知识点
18.已知f(x)=3x2﹣x+4,f[g(x)]=3x4+18x3+50x2+69x+48,那么整系数多项式函数g(x)的各项系数和为( )
正确答案
解析
由题意得g(x)的表达式是二次式,
设g(x)=ax2+bx+c,
∴ f[g(x)]=3(ax2+bx+c)2﹣(ax2+bx+c)+4
=3a2x4+6abx3+(3b2+6ac﹣a2)x2+(6bc﹣b)x+3c2﹣c+4
=3x4+18x3+50x2+69x+48,
∴ 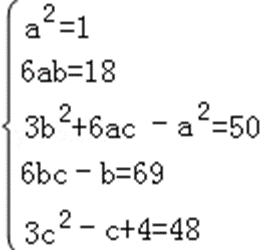
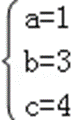
∴ a+b+c=8,
故选:A.
知识点
22.已知二次函数f(x)=ax2+bx+1和函数g(x)=
(1)若g(x)是奇函数,试求f(x)在R上的值域;
(2)若方程g(x)=x有两个不相等的实根,当b>0时,判断f(x)在(﹣1,1)上的单调性;
(3)若方程g(x)=x的两实根为x1,x2f(x)=0的两根为x3,x4,求使x3<x1<x2<x4成立的a的取值范围.
正确答案
解:(1)因为g(x)为奇函数,
所以g(﹣x)=﹣g(x),
又函数g(x)=
则

化简可得b=0,
所以f(x)=ax2+1,定义域为R,
所以函数f(x)的值域为[1,+∞);
(2)由方程g(x)=x整理可得a2x2+bx+1=0,
因为方程g(x)=x有两个不相等的实根,
所以△=b2﹣4a2>0,即|


又因为函数f(x)=ax2+bx+1的对称轴为x=﹣
所以当﹣
当﹣
(3)由

设α为x1与x2中的一个数,
则有
因为x3+x4=﹣

所以有
当a>0时有
所以结合两式可得(a﹣a2)α2<0,
解得:a>1或a<0(舍去).
当a<0时有
所以所以结合两式可得(a﹣a2)α2>0,
解得:0<a<1(舍去).
综上可得a的取值范围为(1,+∞).
解析
解析已在路上飞奔,马上就到!
知识点
11.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.生产某一配件需经过三道工序,设第一.二.三道工序的次品率分别为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列四类函数中,满足性质“对任意的实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.对于实数x.y,定义新运算


正确答案
2010
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析






















