直线与圆的位置关系
共93题

· 直线与圆的位置关系

直线与圆的位置关系
共93题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

已知圆经过点和,且圆心在直线上,则圆的方程为 .

正确答案

解析

略

知识点

直线与圆的位置关系

题型：单选题

单选题 · 5 分

若曲线与曲线有4

个不同的交点，则实数k的取值范围是

正确答案

解析

曲线是以(0，1)为圆心，以1为半径的圆：

曲线即或，直线

恒过定点(0，-1)，即曲线为y轴与恒过定点

(0，-1)的两条直线，如图易得：以直线（或

直线)、y轴与圆共有四个不同的交点，结合图形可知

或，故选D。

知识点

直线与圆的位置关系

题型：简答题

简答题 · 14 分

在平面直角坐标系中，设点(1，0)，直线:，点在直线上移动，是线段与轴的交点, .

(1)求动点的轨迹的方程；

(2)

正确答案

见解析。

解析

知识点

直线与圆的位置关系

题型：单选题

单选题 · 5 分

直线y=kx+1与圆x2+y2﹣2y=0的位置关系是（　　）

A相交

B相切

C相离

D取决于k的值

正确答案

解析

圆x2+y2﹣2y=0 即 x2+（y﹣1）2=1，表示以（0，1）为圆心，半径等于1的圆。

圆心到直线y=kx+1的距离为=0，故圆心（0，1）在直线上，故直线和圆相交，

故选A。

知识点

直线与圆的位置关系

题型：填空题

填空题 · 5 分

如图，圆内的两条弦、相交于，，，若到的距离为，则到的距离为。

正确答案

解析

略

知识点

直线与圆的位置关系

题型：填空题

填空题 · 5 分

如图所示，以直角三角形的直角边为直径作⊙，交斜边于点，过点作⊙的切线，交边于点.则 .

正确答案

解析

略

知识点

直线与圆的位置关系

题型：单选题

单选题 · 5 分

如图,分别与圆相切于点是⊙的割线,连接.则（）

正确答案

解析

由切线长定理知,所以错误。

知识点

直线与圆的位置关系

题型：填空题

填空题 · 5 分

如图⊙O的直径AB=6cm，P是AB延长线上的一点，过P点作⊙O的切线，切点为C，连接AC，且∠CPA=30°，则BP=　　cm。

正确答案

解析

：连接OC，∵CP与⊙O相切于点C，∴OC⊥CP。

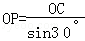
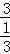
∵OC=3，∠CPA=30°，∴==6。

∴BP=OP﹣OB=6﹣3=3。

故答案为3。

知识点

直线与圆的位置关系

题型：简答题

简答题 · 14 分

设椭圆的左右顶点分别为A（﹣2，0），B（2，0），离心率e=，过该椭圆上任一点P作PQ⊥x轴，垂足为Q，点C在QP的延长线上，且|QP|=|PC|。

（1）求椭圆的方程；

（2）求动点C的轨迹E的方程；

（3）设直线AC（C点不同于A，B）与直线x=2交于点R，D为线段RB的中点，试判断直线CD与曲线E的位置关系，并证明你的结论。

正确答案

见解析。

解析

知识点

直线与圆的位置关系椭圆的定义及标准方程相关点法求轨迹方程

题型：简答题

简答题 · 14 分

设椭圆的左右顶点分别为A（﹣2，0），B（2，0），离心率e=，过该椭圆上任一点P作PQ⊥x轴，垂足为Q，点C在QP的延长线上，且|QP|=|PC|。

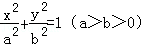
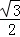
（1）求椭圆的方程；

（2）求动点C的轨迹E的方程；

（3）设直线AC（C点不同于A，B）与直线x=2交于点R，D为线段RB的中点，试判断直线CD与曲线E的位置关系，并证明你的结论。

正确答案

见解析。

解析

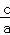
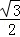
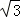
解：（1）由题意，可得a=2，e==，可得c=，∴ b2=a2﹣c2=1，

因此，椭圆的方程为，﹣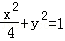

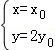
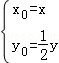
（2）设C（x，y），P（x0，y0），由题意得，即，

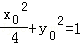
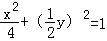
又，代入得，即x2+y2=4。

即动点C的轨迹E的方程为x2+y2=4。

（3）设C（m，n），点R的坐标为（2，t），

∵A、C、R三点共线，∴∥，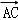

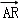
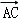
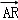
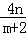
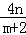
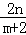
而=（m+2，n），=（4，t），则4n=t（m+2），

∴t=，可得点R的坐标为（2，），点D的坐标为（2，），

∴直线CD的斜率为k==，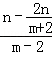

而m2+n2=4，∴﹣n2=m2﹣4，代入上式可得k==﹣，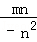

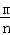
∴直线CD的方程为y﹣n=﹣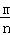（x﹣m），化简得mx+ny﹣4=0，

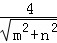
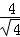
∴圆心O到直线CD的距离d===2=r，

因此，直线CD与圆O相切，即CD与曲线E相切。

知识点

直线与圆的位置关系椭圆的定义及标准方程相关点法求轨迹方程

继续学习学习下一知识点

下一知识点 : 直线与圆相交的性质

百度题库 > 高考 > 理科数学 > 直线与圆的位置关系

扫码查看完整答案与解析