- 直线与圆的位置关系
- 共93题
2.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx+2上至少存在一点使得以该点为圆心,1为半径的圆与圆C 有公共点,则k的最小值是( ).
正确答案
解析
圆C的方程为x2+y2-8x+15=0,整理得(x-4)2+y2=1,即圆C是以(4,0)为圆心,1为半径的圆.又直线y=kx+2上至少存在一点使得以该点为圆心,1为半径的圆与圆C有公共点,∴只需圆C的圆心(4,0)到直线y=kx+2的距离d不大于2即可.
又d=
∴-

知识点
9.已知圆C:x2+y2=16,过点P(2,3)作直线l交圆C于A,B两点,分别过A,B两点作圆C的切线,若两条切线相交于点Q,则点Q的轨迹方程为_______.
正确答案
2x+3y=16
解析
设A(x1,y1),B(x2,y2),Q(m,n),则直线AQ的方程为x1x+y1y=16,直线BQ的方程为x2x+y2y=16,
因为点Q为两直线的交点,所以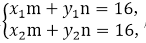
知识点
9.过点P(3,6)作圆
正确答案
x=3,4x-3y+6=0
解析
过点P(3,6)斜率不存在时,直线方程为x=3,
此时与圆
过点P(3,6)斜率存在时,
设方程为y-6=k(x-3),
即kx-y+6-3k=0.
由
得
于是
即4x-3y+6=0.
知识点
4.在平面直角坐标系中,A和B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C周长的最小值为( )
正确答案
解析
设直线2x+y-4=0与圆C相切于点D,∵∠AOB=90°,∴点O在圆C上,则点C与点O间的距离等于点C到直线2x+y-4=0的距离,∴点C在以O为焦点,以直线2x+y-4=0为准线的抛物线上,∴当且仅当O,C,D共线时,圆的直径最小为|OD|。
又|OD|=


知识点
8.设A={(x,y)|x2+(y-1)2=1},B={(x,y)|x+y+m≥0},则使A⊆B成立的实数m的取值范围是________
正确答案
[
解析
集合A是圆x2+(y-1)2=1上的点的集合,集合B是不等式x+y+m≥0表示的平面区域内的点的集合,要使A⊆B,则应使圆被平面区域所包含(如图),



知识点
10.若直线y=x+b与曲线y=3-
正确答案
解析
.C 曲线方程可化简为(x-2)2+(y-3)2=4(1≤y≤3),即表示圆心为(2,3)半径为2的半圆,依据数形结合,当直线y=x+b与此半圆相切时,须满足圆心(2,3)到直线y=x+b的距离等于2,∴




知识点
15.圆C经过点(1,0),且与直线x=-1,y=4都相切,则点C的坐标为_______.
正确答案
(1,2)或(9,-6)
解析
设C(a,b),根据题意有
解得
知识点
1.设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )
正确答案
解析
由题意知,圆的圆心坐标为(3,-1),圆的半径r=2,|PQ|的最小值为圆心到直线x=-3的距离减去圆的半径长,所以|PQ|min=3-(-3)-2=4。
知识点
9.过点(

正确答案
-
解析
如图,



当∠AOB=
此时点O到AB的距离d=
设AB的方程为y=k(x-

由d=


知识点
16.若不等式

正确答案
解析
令y1=

由

结合图象知b=3,a=1,即直线y2与圆y1的交点坐标为(1,2
又因为点(-2,-
所以k=
知识点
扫码查看完整答案与解析






















