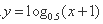
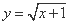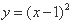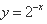函数单调性的判断与证明
共139题

· 函数单调性的判断与证明

函数单调性的判断与证明
共139题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

在下列直线中，与非零向量垂直的直线是

正确答案

解析

略

知识点

函数单调性的判断与证明

题型：单选题

单选题 · 5 分

已知表示平面，m，n表示直线，，给出下列四个结论：

① ；② ；③；④ ，

则上述结论中正确的个数为

正确答案

解析

略

知识点

函数单调性的判断与证明

题型：简答题

简答题 · 14 分

已知函数，，。

（1）若，试判断并用定义证明函数的单调性；

（2）当时，求证：函数存在反函数。

正确答案

见解析

解析

（1）判断：若，函数在上是增函数.

证明：当时，，

在上是增函数.

在区间上任取，设，

所以，即在上是增函数.

（2）因为，所以

当时，在上是增函数，

证明：当时，在上是增函数（过程略）

在在上也是增函数

当时，上是增函数

所以任意一个，均能找到唯一的和它对应，

所以时，存在反函数

知识点

函数单调性的判断与证明反函数

题型：单选题

单选题 · 5 分

在实数集中定义一种运算“”，对任意，为唯一确定的实数，且具有性质：

（1）对任意，；

（2）对任意，。

关于函数的性质，有如下说法：①函数的最小值为；②函数为偶函数；③函数的单调递增区间为。

其中所有正确说法的个数为

正确答案

解析

略

知识点

命题的真假判断与应用函数单调性的判断与证明函数的最值及其几何意义函数奇偶性的判断

题型：单选题

单选题 · 5 分

下列函数中，在区间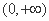上为增函数的是（）

正确答案

解析

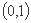
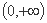
由初等函数的性质得选项B在上递减，选项C、D在为减函数，所以排除B、C、D.

知识点

函数单调性的判断与证明

题型：单选题

单选题 · 5 分

下列函数中，既是奇函数又在区间上单调递增的是

正确答案

解析

略

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：单选题

单选题 · 5 分

下列函数中,在区间上为增函数的是( )

正确答案

解析

函数的图像可由函数的图像向左平移个单位得到,显然满足题意。

知识点

函数单调性的判断与证明

题型：填空题

填空题 · 5 分

关于函数，有下列命题：

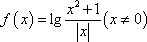
①其图象关于y轴对称；

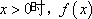
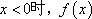
②当是增函数；当是减函数；

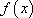
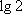
③的最小值是；

④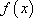在区间上是增函数；

⑤无最大值，也无最小值.

其中所有正确结论的序号是_____________.

正确答案

解析

略

知识点

命题的真假判断与应用函数单调性的判断与证明函数的最值及其几何意义

题型：单选题

单选题 · 5 分

下列函数中，在内单调递减，并且是偶函数的是（）。

正确答案

解析

因为在上是单调递增，故A错；因为在上单调递增且为非奇非偶函数，故B错；同理D错。

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：简答题

简答题 · 14 分

已知函数，其中且.

（1）讨论的单调性；

(2) 若不等式恒成立，求实数取值范围；

（3）若方程存在两个异号实根，，求证：

正确答案

见解析。

解析

(１)的定义域为.

其导数

①当时,,函数在上是增函数;

②当时,在区间上,;在区间(0,+∞)上,。

所以,在是增函数,在(0,+∞)是减函数.

(２)当时, 则取适当的数能使，比如取，

能使, 所以不合题意

当时，令,则

问题化为求恒成立时的取值范围.

由于

在区间上,;在区间上,.

的最小值为,所以只需

即,,

(3)由于存在两个异号根，不仿设，因为,所以

构造函数:()

所以函数在区间上为减函数. ,则,

于是,又,,由在上为减函数可知.即

知识点

函数单调性的判断与证明导数的几何意义导数的运算不等式恒成立问题不等式与函数的综合问题

继续学习学习下一知识点

下一知识点 : 函数单调性的性质

百度题库 > 高考 > 理科数学 > 函数单调性的判断与证明

扫码查看完整答案与解析