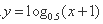
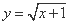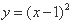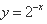- 函数单调性的判断与证明
- 共139题
1
题型:
单选题
|
在下列直线中,与非零向量
正确答案
A
解析
略
知识点
函数单调性的判断与证明
1
题型:
单选题
|
已知 

① 



则上述结论中正确的个数为
正确答案
B
解析
略
知识点
函数单调性的判断与证明
1
题型:
单选题
|
下列函数中,在区间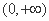
正确答案
A
解析
由初等函数的性质得选项B在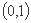
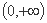
知识点
函数单调性的判断与证明
1
题型:
单选题
|
下列函数中,在区间
正确答案
A
解析
函数


知识点
函数单调性的判断与证明
1
题型:简答题
|
已知函数


(1)讨论
(2) 若不等式

(3)若方程


正确答案
见解析。
解析
(1)

其导数
①当


②当



所以,

(2)当



能使

当

问题化为求

由于







即

(3)由于



构造函数:

所以函数



于是





知识点
函数单调性的判断与证明导数的几何意义导数的运算不等式恒成立问题不等式与函数的综合问题
下一知识点 : 函数单调性的性质
扫码查看完整答案与解析