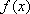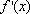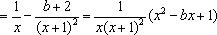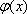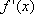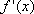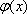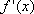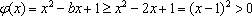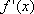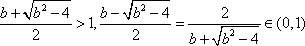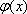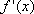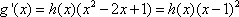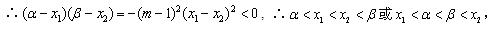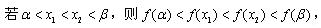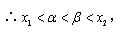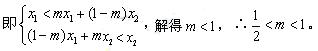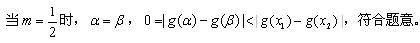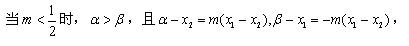- 函数单调性的性质
- 共479题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数

正确答案
解析
由






知识点
设a>0 a≠1 ,则“函数f(x)= ax在R上是减函数 ”,是“函数g(x)=(2-a) 
正确答案
解析
p:“函数f(x)= ax在R上是减函数 ”等价于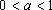
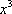
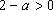
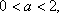
知识点
设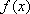
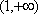
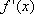

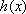

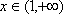
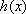
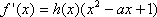
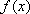
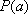
(1)设函数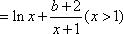

(i)求证:函数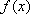
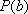
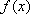
(2)已知函数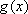
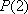
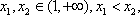
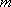
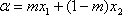
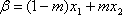

若|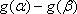
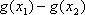
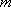
正确答案
见解析。
解析
(1)(i)
∵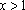
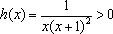
∴函数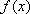
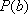
(ii)(方法一)设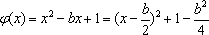
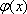
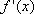
当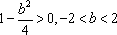
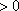
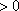
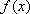
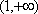
当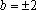
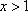
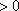
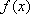
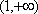
当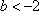
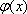

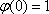
对于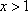
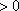
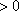
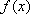
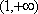
(方法二)当
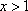
所以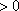
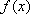
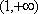
当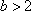
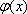
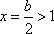
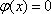
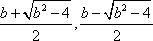
当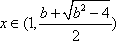
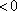
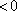
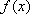
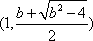
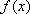

综上所述,当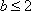
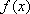
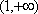
当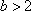
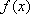
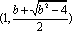
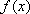
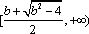
(2)(方法一)由题意,得:
又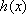
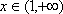

所以对任意的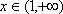
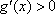
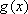
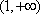
又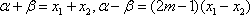
当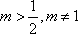
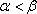
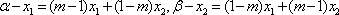
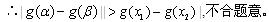
综合以上讨论,得:所求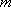
(方法二)由题设知,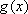
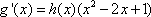
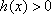
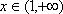
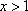
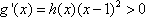
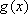
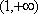
①当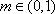
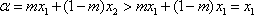
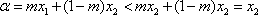
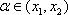
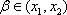
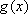
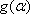
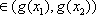
从而有|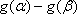
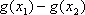
②当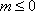
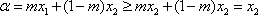
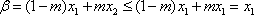
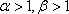
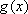
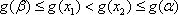
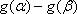
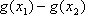
③当
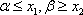
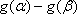
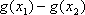
因此综合①、②、③得所求的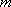
知识点
22,已知







(1)用


(2)求对所有


(3)当


正确答案
见解析
解析
(1)由已知得,交点A的坐标为

(2)由(1)知f(n)=
即知,
当
>2n3+1
当n=0,1,2时,显然
故当a=

所以满足条件的a的最小值是
(3)由(1)知

下面证明:
首先证明:当0<x<1时,
设函数
当
故g(x)在区间(0,1)上的最小值g(x)min=g
所以,当0<x<1时,g(x)≥0,即得
由0<a<1知0<ak<1(

知识点
扫码查看完整答案与解析