- 函数单调性的判断与证明
- 共139题
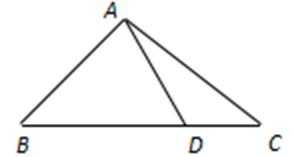
14.如图, 在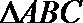
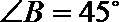
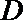
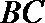
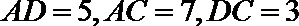
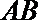
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数f(x)=ax3-(a+b)x2+bx+c,其中a>0,b,c∈R。
(1)若
(2)求证:当0≤x≤1时,|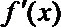
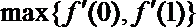
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.已知函数
(1)若函数


(2)如图,设直线


(3)试比较

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若M=



正确答案
解析
假设M<N成立.要证M<N,因为M,N都是非负数,只需证M2<N2,
即证(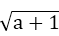

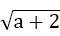

即证
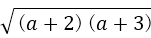
即证4<6,这显然成立,故选A
知识点
2.已知c>b,且f(x)在两个区间[a,b],[c,d]上都是增函数,若补充条件使得f(x)在集合[a,b]∪[c,d]上也是增函数,则应补充的条件是( )
正确答案
解析
由题意,任取
①若x1,x2∈[a,b],由f(x)在[a,b]是增函数,
必有f(x1)<f(x2)成立;
②若x1,x2∈[c,d],由f(x)在[c,d]是增函数,
必有f(x1)<f(x2)成立;
③若a≤x1≤b<c≤x2≤d,
由题设知f(x1)<f(b)且f(c)≤f(x2),
又∵f(b)<f(c),
∴f(x1)<f(x2).
综上所述,f(x)在
知识点
6.设λ,μ都是非零数,且满足



正确答案
解析
由已知可得tan








知识点
20.已知

(1)讨论函数
(2)若函数

①求实数
②求证:
正确答案
见解析
解析
(1)


①当


②当




所以


(2)①由(I)知,当


当







所以

此时,

令

所以


所以
②证法一:
下面证明:当

设





即当






②证法二:
令
则:
所以函数



于是
又

考查方向
解题思路
1利用导数求函数单调性,2根据函数的零点求参数的取值范围
3构造函数求两个零点和的范围
易错点
本题必须注意函数的定义域,以及对参数进行讨论,否则求解错误。
知识点
12.已知定义在R上的奇函数







正确答案
解析
由












考查方向
解题思路
根据题目中的信息画出符合条件的函数的草图,结合草图利用函数的周期性予以解决。
易错点
本题容易因为不理解
知识点
扫码查看完整答案与解析