- 函数单调性的判断与证明
- 共139题
3.下列函数中,在区间
正确答案
解析
A满足在
考查方向
解题思路
直接判断各函数的单调性
易错点
对几个基本函数的图像不熟悉,指数函数和对数函数的性质不熟导致出错
知识点
21.导数已知函数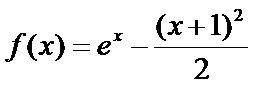
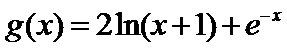
(Ⅰ)当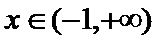
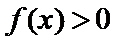
(Ⅱ)若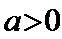
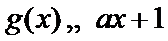
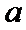
正确答案
(Ⅰ)略
(Ⅱ)1
解析
试题分析:本题属于导数的常规问题,难度较大。函数的单调性、最值、不等式证明问题等等,都可利用导数加以解决。
(Ⅰ)由题意得,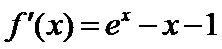
令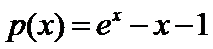

在区间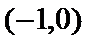
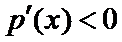

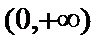
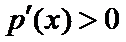

所以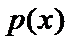
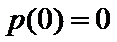
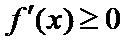
所以函数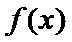
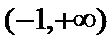
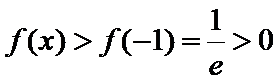
(Ⅱ)令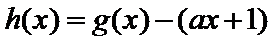
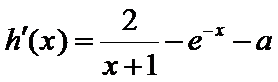
令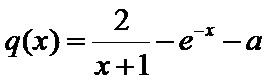
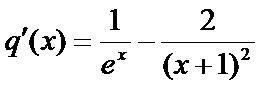
由(1),得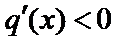
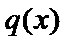
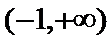
①当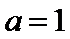
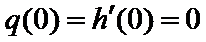
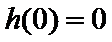
在区间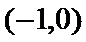
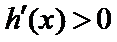
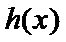
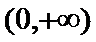
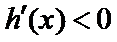
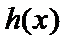
所以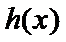
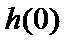
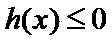
②当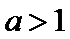
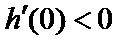
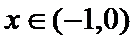

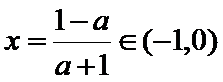
即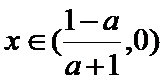
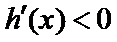
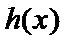
又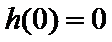
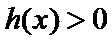

③当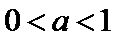
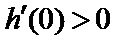
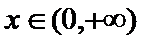
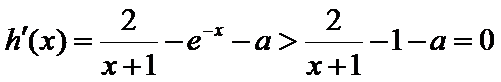
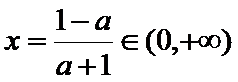
即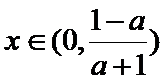
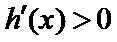
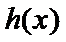
又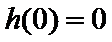
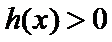
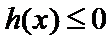
综上,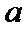

考查方向
解题思路
本题主要考查函数的基本性质、导数的应用等基础知识,
解题步骤如下:
(Ⅰ)把证明不等式问题转化为求函数的最值问题解决;
(Ⅱ)构造函数,分类讨论解决即可。
易错点
(Ⅰ)第一问想不到转化为最小值问题解决;
(Ⅱ)第二问想不到构造函数,利用化归与转化解答。
知识点
10.设函数





正确答案
解析
由题可知,f(x)在

故
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
本题考查三角函数的性质,解题步骤如下:利用减函数的性质求解即可
易错点
本题易在判断单调性上发生错误。
知识点
21.已知a∈R,函数f(x)=xln(﹣x)+(a﹣1)x.
(Ⅰ)若f(x)在x=﹣e处取得极值,求函数f(x)的单调区间;
(Ⅱ)求函数f(x)在区间上的最大值g(a).
正确答案
(Ⅰ)f(x)在(﹣∞,﹣e)上是增函数,在(﹣e,0)上是减函数
(Ⅱ)
解析
(Ⅰ)f'(x)=ln(﹣x)+a,
由题意知x=﹣e时,f'(x)=0,即:f'(﹣e)=1+a=0,∴a=﹣1
∴f(x)=xln(﹣x)﹣2x,f'(x)=ln(﹣x)﹣1
令f'(x)=ln(﹣x)﹣1=0,可得x=﹣e
令f'(x)=ln(﹣x)﹣1>0,可得x<﹣e
令f'(x)=ln(﹣x)﹣1<0,可得﹣e<x<0
∴f(x)在(﹣∞,﹣e)上是增函数,在(﹣e,0)上是减函数,
(Ⅱ)f'(x)=ln(﹣x)+a,∵x∈ , ∴﹣x∈ , ∴ln(﹣x)∈ ,
①若a≥1,则f'(x)=ln(﹣x)+a≥0恒成立,此时f(x)在上是增函数,
fmax(x)=f(﹣e﹣1)=(2﹣a)e﹣1
②若a≤﹣2,则f'(x)=ln(﹣x)+a≤0恒成立,此时f(x)在上是减函数,
fmax(x)=f(﹣e2)=﹣(a+1)e2
③若﹣2<a<1,则令f'(x)=ln(﹣x)+a=0可得x=﹣e﹣a
∵f'(x)=ln(﹣x)+a是减函数,
∴当x<﹣e﹣a时f'(x)>0,当x>﹣e﹣a时f'(x)<0
∴f(x)在(﹣∞,﹣e)上左增右减,
∴fmax(x)=f(﹣e﹣a)=e﹣a,(13分)
综上:
考查方向
解题思路
本题主要考查了导数在研究函数的单调性及在研究单调性的基础上求解其在给定区间上的极值,进而得到最值问题,考查学生综合利用所学知识分析问题和解决问题的能力,属于中档题.解答过程中要用到分类讨论的数学思想,也就是第二问中,通过讨论


易错点
本题了导数在研究函数的单调性及在研究单调性的基础上求解其在给定区间上的极值,进而得到最值问题,在分类讨论时易错。
知识点
6.函数
正确答案
解析
由题得
考查方向
解题思路
本题主要可以从两个方面考虑,第一个利用函数的定义得到函数的单调性,利用函数的图像找到单调性
易错点
主要出现在两个地方:①忽视内层函数的值域为外层函数的定义域,②混淆该函数与对号函数的图像
知识点
18.下列函数中,既是偶函数,又在
① 
② 
③ 
④
正确答案
解析
由图可知,符合要求的函数只有
考查方向
本题主要考查简单三角函数的图像与性质以及函数图像的变换,属于中档题.
解题思路
根据图像变换,先画出



易错点


知识点
12. 已知函数


正确答案
解析
构造函数


因为 



所以
故选A。
考查方向
本题主要考查构造函数比较两个数大小的方法,导数与函数的单调性等知识,是一道综合性较强的问题。
解题思路
(1)根据题意构造函数。
(2)确定函数的单调性。
(3)利用单调性比较大小。
易错点
(1)不能根据题意构造函数。
(2)求函数导数时,出现错误。
知识点
18.下列函数中,既是偶函数,又在
① 
② 
③ 
④
正确答案
解析
① 







② 

③ 

④
考查方向
解题思路
本题考查函数的奇偶性以及三角函数的单调性,可以先化简函数的解析式,再作出判断。
易错点
本题必须注意正切和余切函数的定义域以及分段函数单调性的要求,忽视则会出现错误。
知识点
正确答案
知识点
4.下列函数中,满足“f(xy)=f(x)+f(y)”的单调递减函数是( )
正确答案
解析
对数函数符合条件f(xy)=f(x)+f(y),证明如下:
设f(x)=logax,其中,x>0,a>0且a≠1,
则f(xy)=logaxy=logax+logay=f(x)+f(y),
即对数函数f(x)=logax,符合条件f(xy)=f(x)+f(y),
同时,f(x)单调递减,则a∈(0,1),
综合以上分析,对数函数
故答案为:C.
考查方向
解题思路
1、由f(xy)=f(x)+f(y)判断对数函数符合条件。2、再根据函数的单调性确定选项
易错点
本题在利用抽象函数性质排除选项时易出错。
知识点
扫码查看完整答案与解析





























