- 函数单调性的判断与证明
- 共139题
设函数
正确答案
解析





知识点
对于函数y=f(x),如果存在区间[m,n],同时满足下列条件:
①f(x)在[m,n]内是单调的;
②当定义域是[m,n]时,f(x)的值域也是[m,n]。
则称[m,n]是该函数的“和谐区间”,若函数f(x)=
正确答案
解析
由题意可得函数f(x)=
所以[m,n]⊆(﹣∞,0)或[m,n]⊆(0,+∞),则f(m)=m,f(n)=n,
故m、n是方程
即方程ax2﹣(a+1)x+a=0有两个同号的实数根,注意到mn=
故只需△=(a+1)2﹣4a2>0,解得
结合a>0,可得0<a<1
故选A
知识点
已知矩阵A=

(1)求矩阵A;
(2)若
正确答案
见解析。
解析
(1)由题意,得 
解得a=2,b=4。
所以
(2)解法一:

所以 
解得 
解法二:因为

因为

所以 
知识点
已知
正确答案
解析
两式平方相加得:
∵x、y为锐角,sinx-siny<0,∴x<y,
∴sin(x-y)=
∴tan(x-y)==
知识点
设f(x)是定义在(0,1)上的函数,对任意的y>x>1都有


正确答案
解析
因an=f(



故






=f(

=f(
=f(
故选C。
知识点
已知二阶矩阵





正确答案
见解析
解析
解:设


再由



知识点
若f(x)在R上可导,

正确答案
-18
解析
略
知识点
设矩阵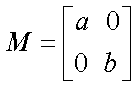
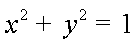

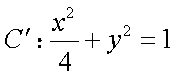
正确答案
见解析。
解析
设曲线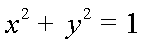
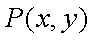
在矩阵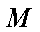
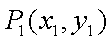
则

又点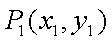
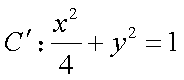
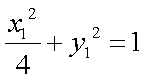
则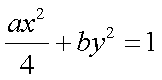
又曲线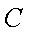
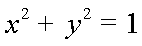
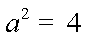
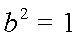
因为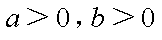
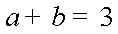
知识点
已知函数







(1)求函数
(2)若锐角


正确答案
(1)
解析
解析:(1)由题意可得





由


函数
由于




知识点
在一个矩形体育馆的一角MAN内(如图所示),用长为a的围栏设置一个运动器材储
存区域,已知B是墙角线AM上的一点,C是墙角线AN上的一点。
(1)若BC=a=10,求储存区域三角形ABC面积的最大值;
(2)若AB=AC=10,在折线MBCN内选一点D,
使DB+DC=a=20,求储存区域四边形DBAC
面积的最大值。
正确答案
见解析
解析
(1)设

所以

当且仅当



(2)由


因为







所以

因此,四边形

知识点
扫码查看完整答案与解析