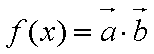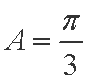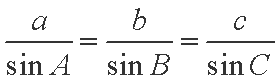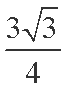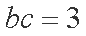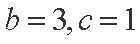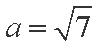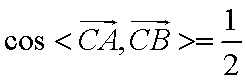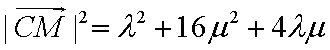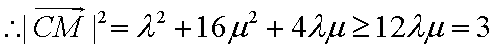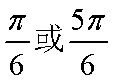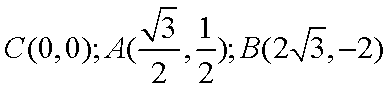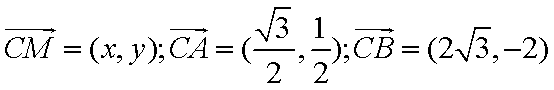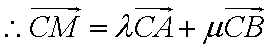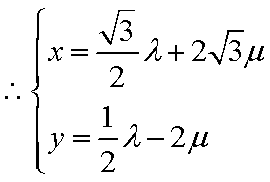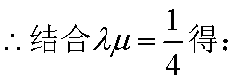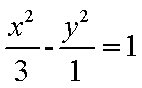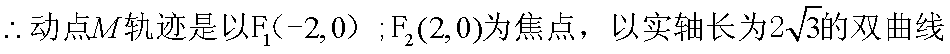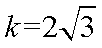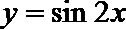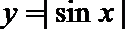- 函数单调性的判断与证明
- 共139题
如图,已知四棱锥






(1)证明

(2)求二面角
正确答案
见解析
解析
解法一:(1)连结




∵底面ABCD是正方形,∴



∴






解法二:(1))以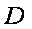


设

∴


则由
∵


(2) 由(1)知





∴
知识点
已知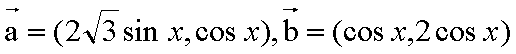
(1)若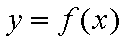

(2)在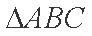
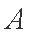
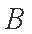

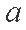
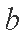

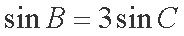
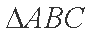
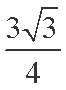

正确答案
见解析。
解析
(1)

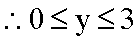
(2)∵ f(A)= 2 ∴
∴ 
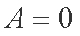
∵ 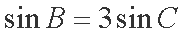
∴ 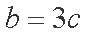
∴ 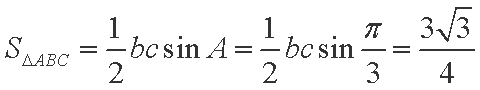
由①和②解得
∵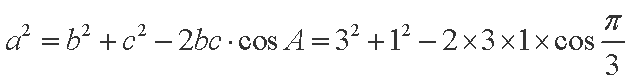
知识点
已知
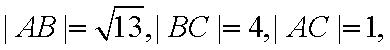
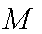
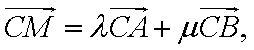
(1)求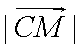
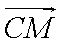

(2)是否存在两定点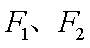
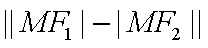
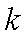
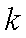
正确答案
见解析。
解析
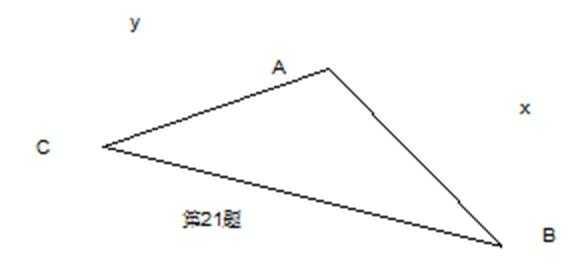
(1)由余弦定理得:
将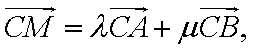

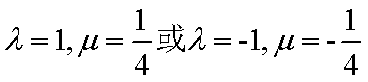
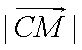
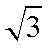
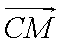
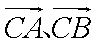
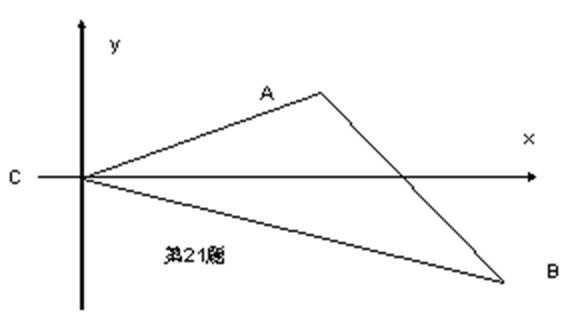
(2)
以顶点C为坐标原点,以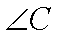

设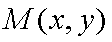

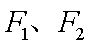
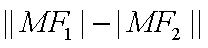
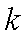
知识点
17.在下列函数中,既是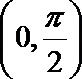
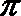
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若行列式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.将正奇数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 下列函数中,在
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)求
(2)画出函数
(3)若关于x 的方程

正确答案
(1)
(2)单调增区间为

(3)
解析
解析已在路上飞奔,马上就到!
知识点
18.已知定义域为

(I)求
(Ⅱ)判断f(x)的单调性并说明理由;
(III)若对任意的


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析