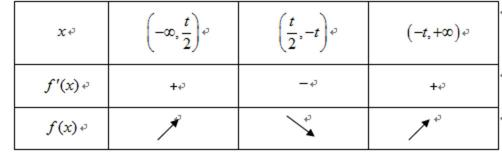
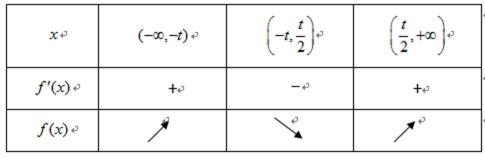
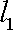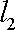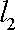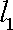- 函数单调性的性质
- 共384题
设α、β是两个不同的平面,m、n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是 ( )
正确答案
解析
因为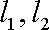
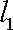
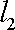
知识点
已知数列






(1)若数列


(2)若




(3)若









证明:
正确答案
见解析
解析
(1)解:由题意得:



(2)因为 


…… 
由于







由于

根据“生成数列”的定义知,数列

(3)证法一:
证明:设数列





由(2)中结论可知 

所以,

所以
证法二:
因为 
所以 
所以欲证

对于数列

因为 


…… 
由于




相加得


设数列



所以 

同理可证,

所以 
知识点
若




正确答案
解析




知识点
执行如图所示的程序框图,输出的S值为
正确答案
解析
第一次循环为:




知识点
已知向量



(1) 求正数ω;
(2) 若函数f(x)的图像向左平移

正确答案
见解析。
解析
(1)f(x)=(2cosωx,-1)·(sinωx-cosωx,2)+3……………………………………………1分
=2cosωx(sinωx-cosωx)+1………………………………………………………2分
=2sinωxcosωx-2cos2ωx+1………………………………………………………3分
=sin2ωx-cos2ωx……………………………………………………………… 4分
=

∵T=π,且ω>0,∴ω=1.……………………………………………………… 6分
(2) 由(1)知:f(x)= 

g(x)= 


∴2kπ-

∴kπ- 


知识点
如图四棱锥








(1)求证:

(2)试在线段





正确答案
见解析
解析
解:(1)证明:







(2)设




















设









知识点
已知中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2, 2),且抛物线y2=
(1) 求椭圆E的方程;
(2) 垂直于OC的直线l与椭圆E交于A、B两点,当以AB为直径的圆P与y轴相切时,求直线l的方程和圆P的方程.
正确答案
见解析。
解析
(1) 设椭圆E的方程为
则
∵抛物线
∴
又a2=b2+c 2 ③
由①、②、③得a2=12,b2=6……………………………………………… 5分
所以椭圆E的方程为
(2) 依题意,直线OC斜率为1,由此设直线l的方程为y=-x+m,………… 7分
代入椭圆E方程,得3x2-4mx+2m2-12=0. ………………………………… 8分
由Δ=16m2-12(2m2-12)=8(18-m2),得m2<18. ………………………………9分 记A(x1,y1)、B(x2,y2),则x1+x2=

圆P的圆心为
半径
当圆P与y轴相切时,

即
当m=3时,直线l方程为y=-x+3,此时,x1+x2=4,圆心为(2,1),半径为2,
圆P的方程为(x-2)2+(y-1)2=4;……………………………………………13分
同理,当m=-3时,直线l方程为y=-x-3,
圆P的方程为(x+2)2+(y+1)2=4…………………………………………… 14 分
知识点
为了了解某市工人开展体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂。
(1)从A,B,C区中分别抽取的工厂个数;
(2)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,计算这2个工厂中至少有1个来自A区的概率。
正确答案
见解析。
解析
(I)工厂总数为18+27+18=63,样本容量与总体中的个体数比为
所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2。…………6分
(2)设A1,A2为在A区中的抽得的2个工厂,B1,B2,B3为在B区中抽得的3个工厂,
C1,C2为在C区中抽得的2个工厂。 …………7分
这7个工厂中随机的抽取2个,全部的可能结果有
随机的抽取的2个工厂至少有一个来自A区的结果有A1,A2),A1,B2),A1,B1),
A1,B3)A1,C2),A1,C1), …………9分
同理A2还能给合5种,一共有11种。 …………10分
所以所求的概率为
知识点
已知函数
(1)求
(2)求
(3)求

正确答案
见解析。
解析
(1)
所以最小正周期为
(2) 由 
整理,得

(3)当

故当x=0时,

知识点
已知函数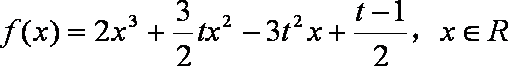
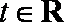
(1)当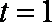
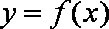
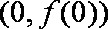
(2)当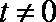
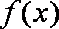
(3)证明:对任意的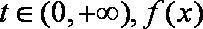
正确答案
见解析。
解析
(1)当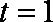
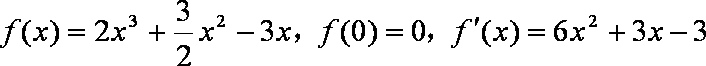
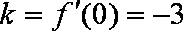
所以曲线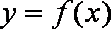
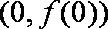
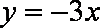
(2)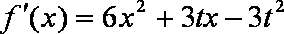
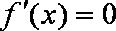
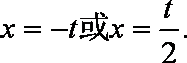
因为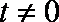
(1)若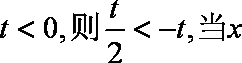
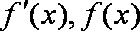
所以,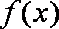
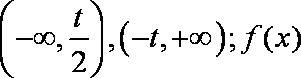
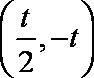
(2)若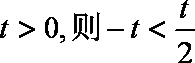
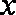
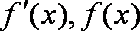
所以,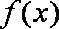

………………………………………………………………………………………10分
(3)由(2)可知,当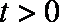
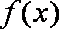

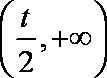
以下分两种情况讨论:
(1)当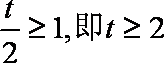
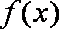
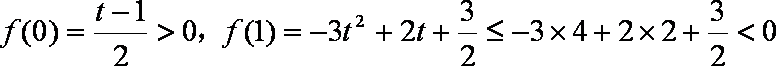
所以对任意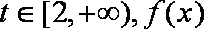
(2)当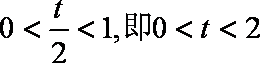
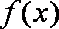


若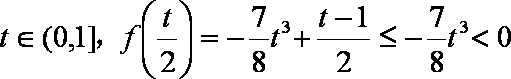
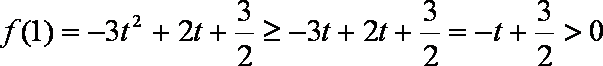
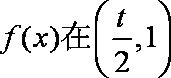
若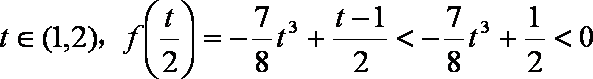
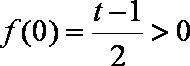
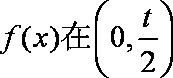
所以,对任意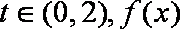
综上,对任意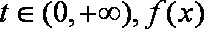
知识点
扫码查看完整答案与解析