- 函数单调性的性质
- 共384题
若关于x的不等式ax>b的解集为

正确答案
解析
∵ ax>b的解集为
∴

∴

所以不等式

即:

知识点
抛物线y2=2px(p>0)的焦点为F,倾斜角为60°的直线l过点F且与抛物线的一个交点为A,|AF|=3,则抛物线的方程为( )
正确答案
解析
过A作AB⊥x轴于B点,则
Rt△ABF中,∠AFB=60°,|AF|=3
∴|BF|=


设A的坐标为(x0,
得

∴抛物线的方程为y2=3x或y2=9x
故选:D
知识点
已知平面区域


正确答案
解析
如右图所示,
设直线




∴
扇形
∴阴影部分面积
∴
显然








故答案为:
各自的面积,即可得到

知识点
已知数列


(1)求数列

(2)记

正确答案
见解析
解析
(1)当

当

又
∴
(2)∵

当
∴



知识点
已知函数




(1)求a,b,c,d的值;
(2)若

正确答案
(1)a=4,b=2,c=2,d=2(2)
解析
解析:(1)由已知得
而
故
(2)令
则
因
令

① 若










故当


② 若









若



综上:

知识点
为了降低能损耗,最近上海对新建住宅的屋顶和外墙都要求建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=(0≤x≤10),若不建隔热层,每年能消耗费用为8万元,设f(x)为隔热层建造费用与20年的能消耗费用之和。
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
正确答案
见解析
解析
(1)当x=0时,C(0)=8,即=8,所以k=40,
所以C(x)=,
所以f(x)=6x+=6x+(0≤x≤10)。
(2)f(x)=2(3x+5)+-10
≥2-10
=70,
当且仅当2(3x+5)=,即x=5时,等号成立,因此最小值为70,
所以,当隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元。
知识点
如图,在平面直角坐标系














(1)求椭圆
(2)证明点
(3)求
正确答案
见解析。
解析
(1)由题意得

解得



(2)设




所以直线

消去


故点

(3)由(2)得点

又


所以点



将


所以






知识点
设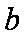
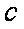
(1)求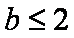
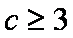
(2)求函数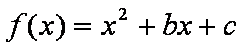
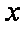
正确答案
(1)P=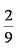
解析
解析:(1)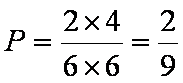
(2)
当

知识点
为了调查某厂2000名工人生产某种产品的能力,随机抽查了聊位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],得到如题(16)图所示的频率分布直方图,已知生产的产品数量在[20,25)之间的工人有6位。
(1)求m;
(2)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,求这2位工人不在同一组的概率。
正确答案
见解析
解析
(1)由题得,
∴
(2)由题得,



从这两组中抽取



∴
知识点
已知函数
正确答案
解析
由函数

由
故函数y=f[f(x)]+1共4个零点,
故选A。
知识点
扫码查看完整答案与解析