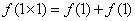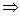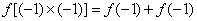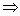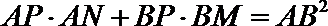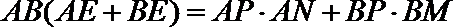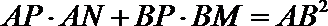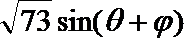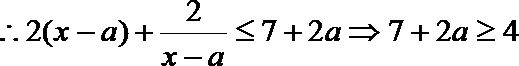- 函数单调性的性质
- 共384题
17.已知数列








(Ⅰ) 求数列


(Ⅱ)设


正确答案
解:(Ⅰ)∵


∴ 




再由
∴

∴
(Ⅱ)


解析
解析已在路上飞奔,马上就到!
知识点
18.已知向量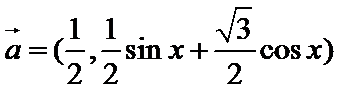
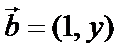
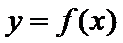
(1)求函数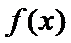
(2)已知锐角 △ABC 中的三个内角分别为 A、B、C,若有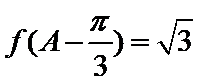
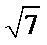
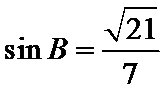
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在各项均为正数的等比数列{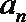
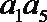
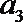
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数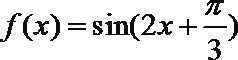
①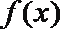
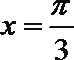
②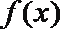
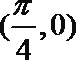
③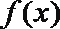
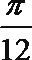
④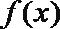
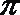
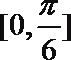
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知:函数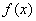
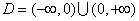
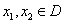
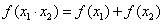
(1)求: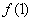
(2)判断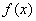
(3)如果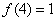
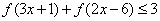
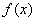
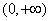
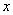
正确答案
(1)解:令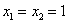
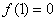
(2)证明:令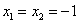
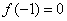
令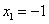
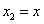

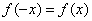
∴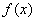
(3)∵
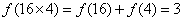
∴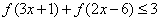
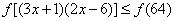
∵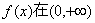
∴(1)等价于不等式组: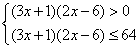
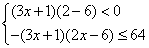
则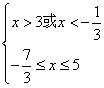

解析
解析已在路上飞奔,马上就到!
知识点
19.定义在R上的单调函数f(x)满足f(3)=log
(1)求证f(x)为奇函数;
(2)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知向量a



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答
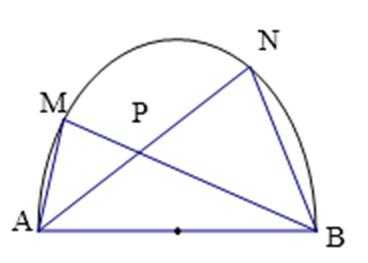
22.选修4—1 几何证明选讲
在直径是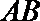
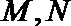
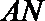
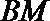
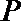
求证:
23.选修4—4 极坐标系与参数方程
已知圆方程为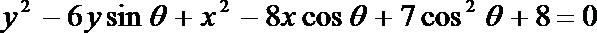
(1)求圆心轨迹的参数方程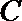
(2)点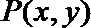
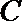
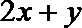
24.选修4—5 不等式选讲
(1)已知关于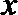
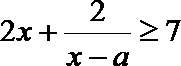
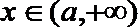
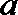
(2)已知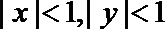

正确答案
22.
证明:作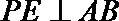
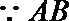
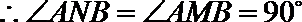
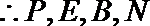
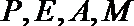
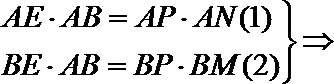
即
23.
(1)将圆的方程整理得:(x-4cos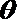
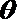
则
(2)2x+y=8cos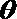
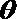
∴ -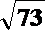
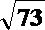
24.
(1)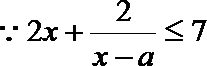
(2)因为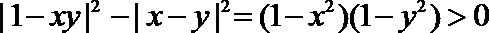
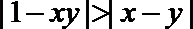
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析