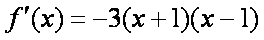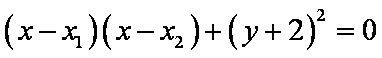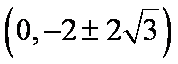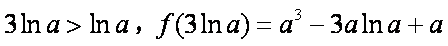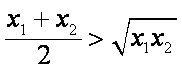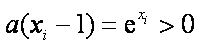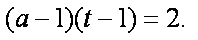- 函数单调性的性质
- 共384题
数列
若存在正整数k,使
正确答案
解析


知识点
已知

正确答案
﹣7
解析
∵

∴
两式相比得
即4sinx+4cosx=3sinx﹣3cosx,
∴sinx=﹣7cosx,
∴tanx=﹣7,
知识点
如图,在△ABC中,|





(1)求C的大小;
(2)设D为AB的中点,求CD的长。
正确答案
见解析。
解析
(1)依题意BC=3,CA=5,AB=7,
由余弦定理,得cosC=

∵0<C<π,
∴C=
(2)由余弦定理,得cosA=

在△ADC中,AD=
根据余弦定理得:CD2=AC2+AD2﹣2AC×AD×cosA=
则CD=
知识点
已知函数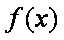
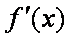
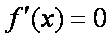
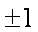
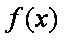
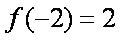
(1)求函数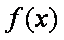
(2)若函数在开区间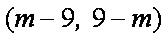
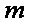
(3)设函数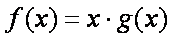
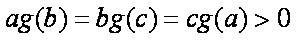
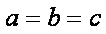
正确答案
见解析
解析
(1)设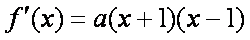
则可设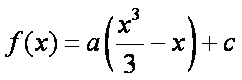
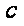
因为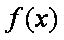
所以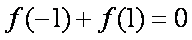
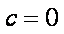
由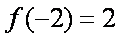
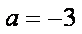
所以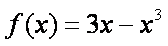
(2)由(1)得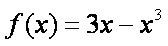
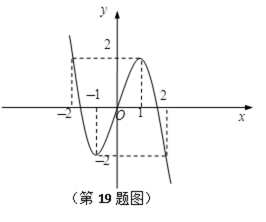
由题意得,三次函数在开区间上存在的最大值与最小值必为极值(如图),
又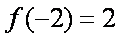
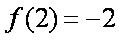
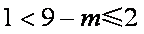
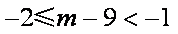
解得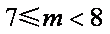
(3)题设等价与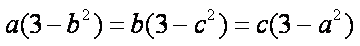
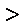
所以a,b,c均小于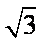
假设在a,b,c中有两个不等,不妨设a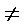
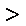
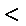
若a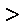
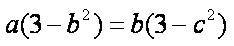
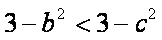
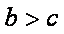
又由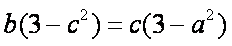
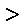
于是a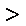
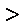
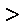
同理,若a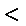
故假设不成立,所以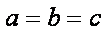
知识点
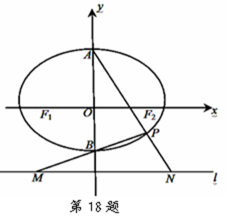
如图,椭圆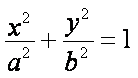
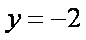
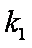
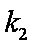
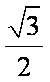
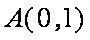
(1)求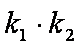
(2)求MN的最小值;
(3)随着点P的变化,以MN为直径的圆是否恒过定点,
若过定点,求出该定点,如不过定点,请说明理由。
正确答案
见解析
解析
(1)因为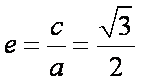
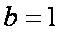
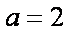
所以椭圆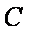
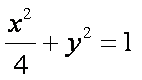
设椭圆上点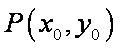
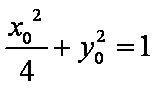
所以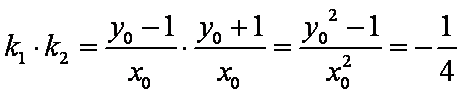
(2)因为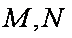
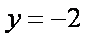
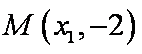
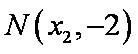
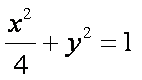
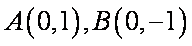
所以
又由(1)知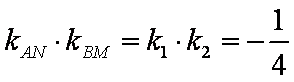
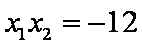
不妨设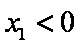
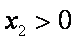

所以当且仅当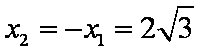
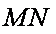
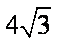
(3)设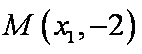
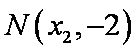
则以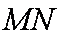
即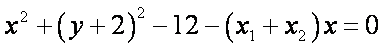
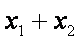
所以有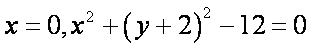
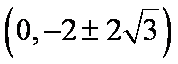
所以,无论点P如何变化,以MN为直径的圆恒过定点
知识点
已知函数f(x)=(2x2-4ax)lnx+x2(a>0)。
(1)求f(x)的单调区间;
(2)若对任意的x∈[1,+∞),不等式(2x-4a)lnx>-x恒成立,求a的取值范围。
正确答案
见解析
解析
(1)求导数,得
f ′(x)=(4x-4a)lnx++2x=4(x-a)(lnx+1)(x>0),
令f ′(x)=0,解得x=a,或x=。
① 当0<a<时,x变化时,f ′(x),f(x)的变化情况如下表:
此时f(x)的单调递增区间为(0,a),(,+∞);单调递减区间为(a,)。
② 当a=时,f ′(x)≥0,此时f(x)的单调递增区间为(0,+∞),没有单调递减区间。
③ 当a>时,x变化时,f ′(x),f(x)的变化情况如下表:
此时f(x)的单调递增区间为(0,),(a,+∞);单调递减区间为(,a)。
(2)由(2x-4a)lnx>-x(x≥1),得(2x2-4ax)lnx+x2>0,
即f(x)>0对x≥1恒成立。
由(1)可知,
当0<a≤时,f(x)在[1,+∞)上单调递增,则f(x)min=f(1)>0恒成立;
当<a≤1时,f(x)在[1,+∞)上单调递增,则f(x)min=f(1)=1>0恒成立;
当a>1时,f(x)在(1,a)上单调递减,在(a,+∞)上单调递增,则f(x)min=f(a)>0,即(2a2-4a2)lna+a2>0,解得1<a<。
综上可知,a的取值范围为(0,)。
知识点
在直角坐标系xOy中,已知A(﹣1,0),B(0,1),则满足PA2﹣PB2=4且在圆x2+y2=4上的点P的个数为 。
正确答案
2
解析
设P(x,y),
∵A(﹣1,0),B(0,1),
由PA2﹣PB2=4,得(x+1)2+y2﹣x2﹣(y﹣1)2=4。
整理得:x+y=2。
联立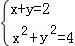
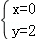
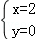
∴P点坐标为(0,2)或(2,0)。
即满足条件的P点的个数为2。
知识点
已知函数
(1)若


(2)若



正确答案
见解析
解析
(1)因为












所以


(2)当


当


当


当




当


当



所以,当


当


当


综上所述,当




所以函数



知识点
设函数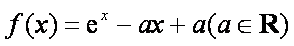
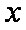
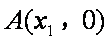
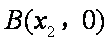
(1)求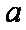
(2)证明: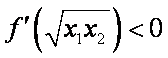
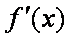
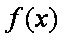
(3)设点C在函数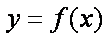
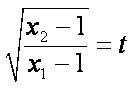
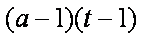
正确答案
见解析。
解析
(1)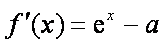
若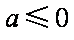
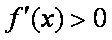
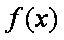
所以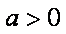
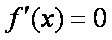
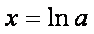
当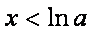
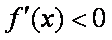
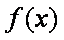
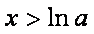
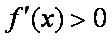
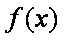
于是当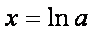
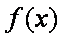
因为函数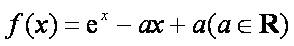
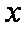
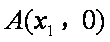
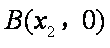
所以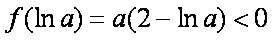
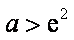
此时,存在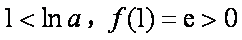
存在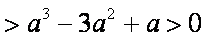
又由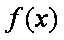
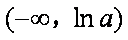
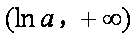
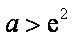
(2)因为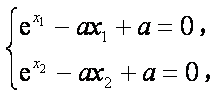
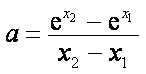
记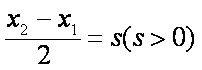

设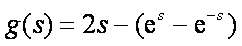
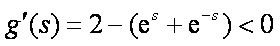
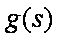
则有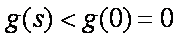
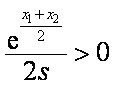
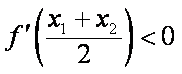
又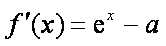
所以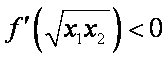
(3)依题意有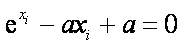
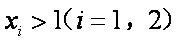
于是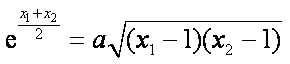
所以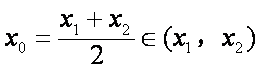
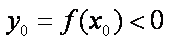
由直角三角形斜边的中线性质,可知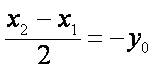
所以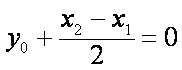
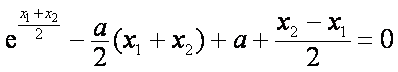
所以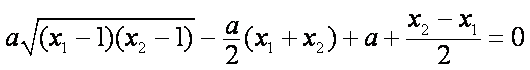
即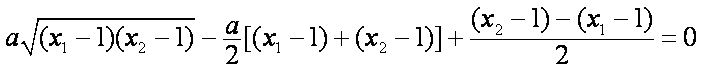
因为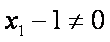

又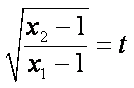
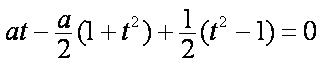
即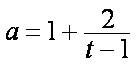
知识点
设t∈R,[t]表示不超过t的最大整数,则在平面直角坐标系xOy中,满足[x]2+[y]2=13的点P(x,y)所围成的图形的面积为 。
正确答案
8
解析
由题意可得:方程:[x]2+[y]2=13,
当x,y≥0时,[x],[y]的整数解为(2,3),所以此时x可能取的数值为:2。
所以当|[x]|=2时,2≤x<3,或者﹣2≤x<﹣1,|[y]|=3,3≤y<4,或者﹣3≤y<﹣2,围成的区域是8个单位正方形,
所以满足[x]2+[y]2=13的点P(x,y)所成的图形面积为8。
知识点
扫码查看完整答案与解析