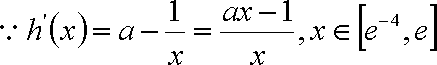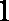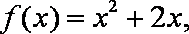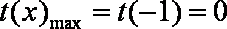- 函数单调性的性质
- 共384题
设函数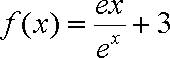
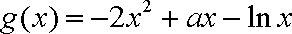
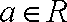
(1)若函数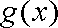
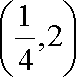
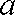
(2)若对任意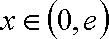
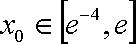
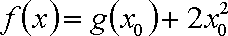
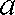
正确答案
见解析
解析
(1)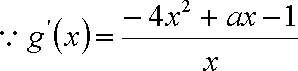
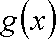
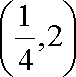
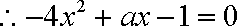
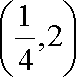
即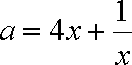
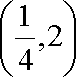
令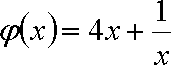
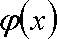
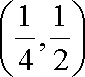
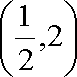
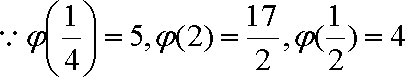
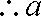
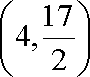
(2)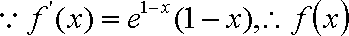
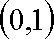
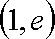
且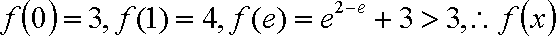
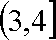
记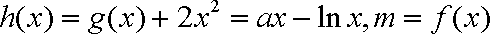
原问题等价于: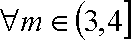
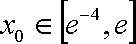
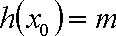
① 当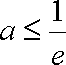
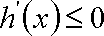
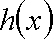
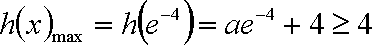
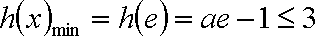
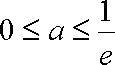
② 当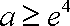
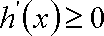
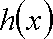
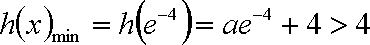
③ 当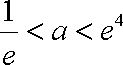
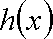
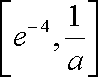
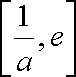
且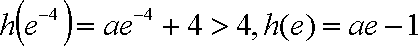
要满足条件则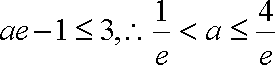
综上所述: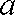
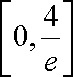
知识点
在函数




正确答案
解析
对于函数f(x)=x上的点列(xn,yn),有yn=


知识点
如图,已知P是边长为2的正三角形的边BC上的动点,则
正确答案
解析
设BC的中点为D,


知识点
若函数


正确答案
解析
作图分析知当

知识点
过抛物线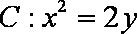
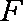
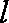
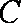
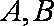
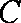
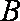
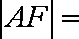
正确答案
解析
设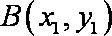
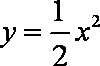
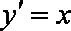



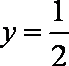
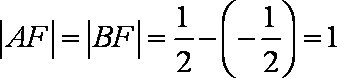
知识点
路灯距地平面为8m,一个身高为1.75m的人以
正确答案
解析
如图,路灯距地平面的距离为DC,人的身高为EB,设人从C点运动到B处路程为x米,时间为t(单位:秒),AB为人影长度,设为y,则∵BE∥CD,∴
∴


∴y=

∵y′=

知识点
在等比数列






(1)求

(2)若对任意的


正确答案
见解析。
解析
(1)设



∴
∴
-------------------------------------5分
(2)
①当


即
而



∴
②当


即
而

∴
综上,实数

知识点
双曲线


正确答案
解析
由题知

知识点
对于实数







①

(1)若

(2)当



正确答案
(1)

解析
(1)若

(2)
当




①当

(
②当

(
综上,
知识点
已知函数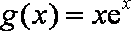
(1)求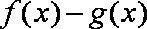
(2)当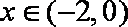
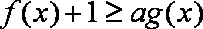
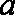
正确答案
见解析
解析
(1)令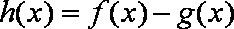
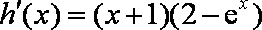

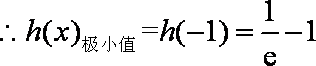
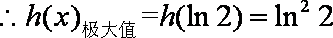
(2)由已知,当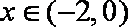

即
令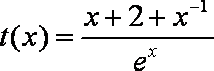

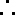
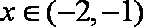
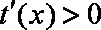
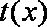
当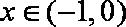
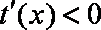
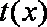
故当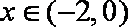
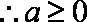
知识点
扫码查看完整答案与解析