- 三角函数的图象与性质
- 共712题
7.函数f(x)=(

正确答案
知识点
7.函数

正确答案
解析
由题意可知T=



考查方向
解题思路
1、利用相邻的零点与对称轴之间的距离求出


易错点
本题易于在求解
知识点
已知





正确答案
解析
由







考查方向
本题主要考查了矩阵的概念,三角函数图像与性质的综合应用
易错点
函数平移的对象是x,这是解决函数平移的问题的关键
知识点
15.已知函数

(Ⅰ)求
(Ⅱ)设


正确答案
(Ⅰ)



解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(Ⅰ)解:

所以函数

由

得
所以函数


(注:或者写成单调递增区间为

(Ⅱ)解:由题意,得
因为函数

所以

所以

解得

又因为
所以

考查方向
本题主要考查了三角恒等变换以及三角函数的图象与性质,三角函数的性质的考查主要分以下几类:
1.三角函数的定义域,
2.三角函数的单调性与最值,
3.三角函数的周期性,
4.三角函数的奇偶性或对称性.
解题思路
本题考查三角恒等变换、三角函数的图象与性质,解题步骤如下:1.利用二倍角公式和配角公式将函数




易错点
1、第一问中的单调递增区间易错误写成集合的形式,或丢掉“
2、第二问中易利用

知识点
16.已知函数

(Ⅰ)求函数
(Ⅱ)若

正确答案
(Ⅰ)函数
(Ⅱ)

解析
本题第二问特别要注意:一定要结合函数的定义域正确书写增区间.

所以函数

(Ⅱ)解:由

得
所以函数


所以当



(注:或者写成增区间为

考查方向
解题思路
本题主要考查正、余弦的二倍角公式及
1、把

2、由

3、最后通过
易错点
本题体现了三角函数部分的基本的解题思想方法,为学生非常熟悉的题型对于第二问可能由于思维定势审题不全忽略

知识点
(本小题满分13分)
已知函数

(Ⅰ)若


(Ⅱ)若



正确答案
考查方向
易错点
1、本题在第一问
知识点
15.已知函数
(Ⅰ)求函数
(Ⅱ)求函数

正确答案
(Ⅰ)
(Ⅱ)0
解析
(Ⅰ)因为



(Ⅱ)因为


当


当


因为
所以函数

考查方向
本题主要考察了三角函数的图象与性质,属于中档题,是高考的热点,解决此类题的关键:一是会化简,熟悉三角恒等变形公式;二是会用性质,熟悉单调性、周期性、对称性、和最值问题。
易错点
1、本题易在化简的过程汇总发生错误,导致最小正周期算错 。
2、单调性分析不全面,导致题目无法进行。
知识点
4.已知函数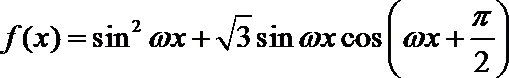
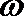

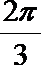
正确答案
解析
∵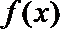
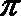
∴
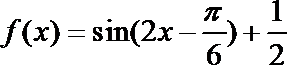
∵
∴

所以答案选A
考查方向
本题主要考查了三角函数的周期和值域
解题思路
利用利用辅助角公式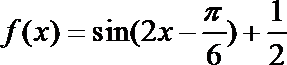
易错点
利用辅助角公式化简函数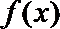
知识点
17.设函数
(1)求函数
(2)若





正确答案
(1)


(2)

解析
试题分析:本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关三角函数的知识,即可解决本题,解析如下:
试题解析:(1)
∴函数f(x)的最小正周期
当

当

(2)因为

∴


∵
由余弦定理得:
∴
考查方向
解题思路
(1)先用两角和与差的正弦化简
(2)先根据解析式求得角


易错点
相关知识点不熟容易证错。
知识点
(18分)(2015•上海)对于定义域为R的函数g(x),若存在正常数T,使得cosg(x)是以T为周期的函数,则称g(x)为余弦周期函数,且称T为其余弦周期.已知f(x)是以T为余弦周期的余弦周期函数,其值域为R.设f(x)单调递增,f(0)=0,f(T)=4π.
(1)验证g(x)=x+sin
(2)设a<b,证明对任意c∈[f(a),f(b)],存在x0∈[a,b],使得f(x0)=c;
(3)证明:“u0为方程cosf(x)=1在[0,T]上得解,”的充分条件是“u0+T为方程cosf(x)=1在区间[T,2T]上的解”,并证明对任意x∈[0,T],都有f(x+T)=f(x)+f(T).
正确答案
解:(1)g(x)=x+sin
∴

∴g(x)是以6π为周期的余弦周期函数;
(2)∵f(x)的值域为R;
∴存在x0,使f(x0)=c;
又c∈[f(a),f(b)];
∴f(a)≤f(x0)≤f(b),而f(x)为增函数;
∴a≤x0≤b;
即存在x0∈[a,b],使f(x0)=c;
(3)证明:若u0+T为方程cosf(x)=1在区间[T,2T]上的解;
则:cosf(u0+T)=1,T≤u0+T≤2T;
∴cosf(u0)=1,且0≤u0≤T;
∴u0为方程cosf(x)=1在[0,T]上的解;
∴“u0为方程cosf(x)=1在[0,T]上得解”的充分条件是“u0+T为方程cosf(x)=1在区间[T,2T]上的解”;下面证明对任意x∈[0,T],都有f(x+T)=f(x)+f(T):
①当x=0时,f(0)=0,∴显然成立;
②当x=T时,cosf(2T)=cosf(T)=1;
∴f(2T)=2k1π,(k1∈Z),f(T)=4π,且2k1π>4π,∴k1>2;
1)若k1=3,f(2T)=6π,由(2)知存在x0∈(0,T),使f(x0)=2π;
cosf(x0+T)=cosf(x0)=1⇒f(x0+T)=2k2π,k2∈Z;
∴f(T)<f(x0+T)<f(2T);
∴4π<2k2π<6π;
∴2<k2<3,无解;
2)若k1≥5,f(2T)≥10π,则存在T<x1<x2<2T,使得f(x1)=6π,f(x2)=8π;
则T,x1,x2,2T为cosf(x)=1在[T,2T]上的4个解;
但方程cosf(x)=1在[0,2T]上只有f(x)=0,2π,4π,3个解,矛盾;
3)当k1=4时,f(2T)=8π=f(T)+f(T),结论成立;
③当x∈(0,T)时,f(x)∈(0,4π),考查方程cosf(x)=c在(0,T)上的解;
设其解为f(x1),f(x2),…,f(xn),(x1<x2<…<xn);
则f(x1+T),f(x2+T),…,f(xn+T)为方程cosf(x)=c在(T,2T)上的解;
又f(x+T)∈(4π,8π);
而f(x1)+4π,f(x2)+4π,…,f(xn)+4π∈(4π,8π)为方程cosf(x)=c在(T,2T)上的解;
∴f(xi+T)=f(xi)+4π=f(xi)+f(T);
∴综上对任意x∈[0,T],都有f(x+T)=f(x)+f(T).
知识点
扫码查看完整答案与解析