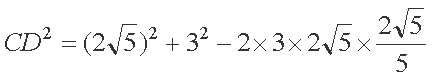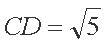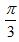- 三角函数的图象与性质
- 共712题
已知






(1)求
(2)当


正确答案
(1)
解析
(1)因为
即

所以 
(2)由
故
由


由正弦定理,

故
知识点
在△ABC中,已知A=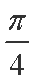

(1)求cosC的值;
(2)若BC=2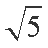
正确答案
见解析。
解析
(1)
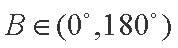
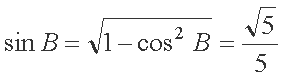
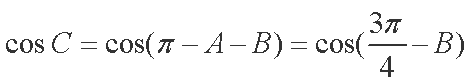
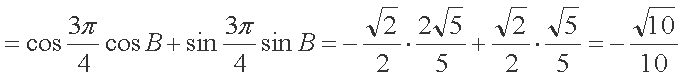
(2)由(1)可得
由正弦定理得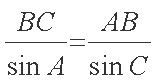
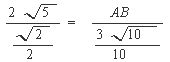
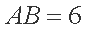
在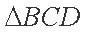

知识点

正确答案
解析



知识点
设△ABC的内角A,B,C所对的边分别为a,b,c,已知a=1,b=2,
(1)求边c的长;
(2)求cos(A﹣C)的值。
正确答案
见解析
解析
解:(1)由
因为a=1,b=2,所以
所以c2=a2+b2﹣2abcosC=4,
所以c=2
(2)因为
所以sinC=

所以

因为a<c,所以A<C,故A为锐角,所以cosA=
所以cos(A﹣C)=cosAcosC+sinAsinC
=
知识点
已知锐角
(1)求角A的大小;
(2)求
正确答案
(1)
解析
解析:(1)由已知条件及余弦定理得
∴

(2)
=
=2

知识点
在△




正确答案
解析
由




知识点
设









正确答案
解析
识别条件:偶函数,偶函数说明啥?定义:f(-x)=f(x)恒成立!还有图像关于y轴对称!
这就是转化一念间 对任意的

周期函数为4 在



设
知识点
在△
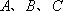
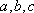
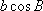
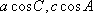
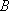
正确答案
解析
略
知识点
已知中心为O的正方形ABCD的边长为2,点M,N分别为线段BC,CD上的两个不同点,且|

正确答案
解析
如图所示,建立平面直角坐标系。
设M(2,b),N(a,2),∵

又O(1,1),∴
令a+b﹣2=t,则目标函数b=﹣a+2+t,
作出可行域

①当目标函数与圆弧相切与点P时,

②当目标函数经过点EF时,t=2+1﹣2=1取得最大值。
∴

故答案为
知识点
已知集合


正确答案
解析
由于集合M、N都是数集,所


知识点
扫码查看完整答案与解析