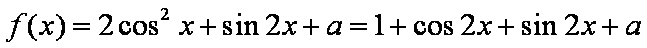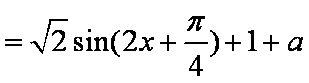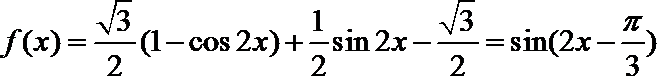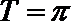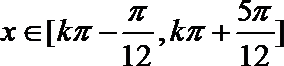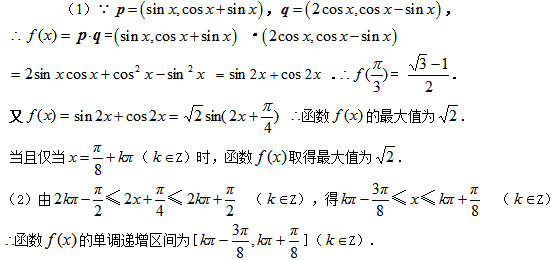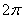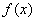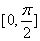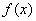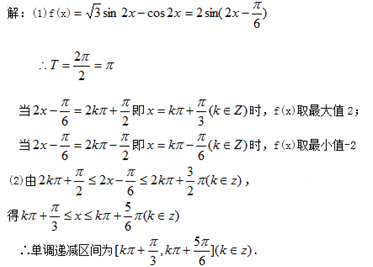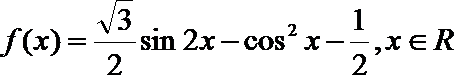- 三角函数的图象与性质
- 共712题
设函数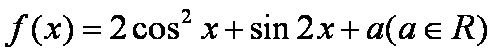
(1)求函数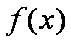
(2)当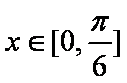
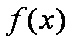
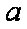
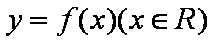
正确答案
见解析
解析
解:(1)
则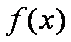
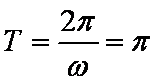
且当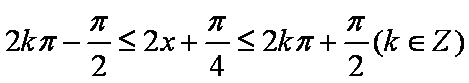
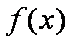
即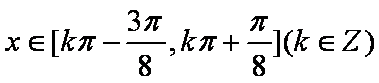
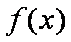
(2)当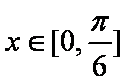
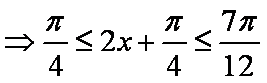
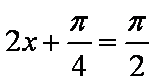
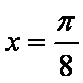
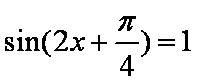
所以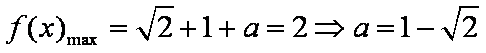
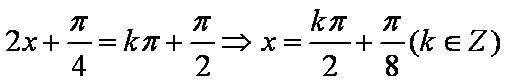
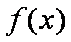
知识点
16.设函数

(Ⅰ)求
(Ⅱ)若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数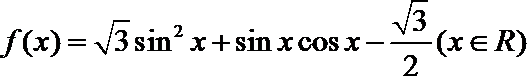
(1)求函数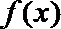
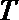
(2)在△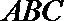
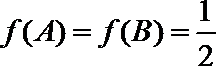
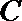
正确答案
(1)
所以周期
由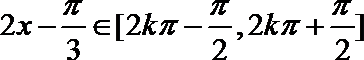
得
即函数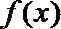
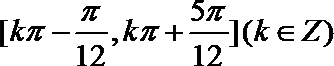
(2)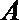
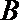
所以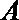
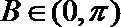
由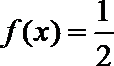
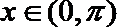
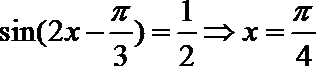
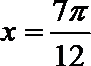
又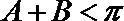
所以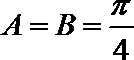
或
所以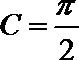
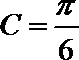
解析
解析已在路上飞奔,马上就到!
知识点
16.某同学用“五点法”画函数
(1)请写出上表的


(2)将







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数①

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.定义域是一切实数的函数






①

②“
③

其中正确结论的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 设函数f(x)=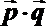
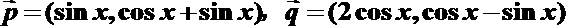
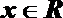
(1)求f(
(2)求函数f(x)的单调递增区间。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数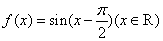
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数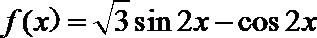
(1)求函数
(2)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(1)求函数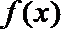
(2)确定函数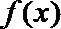
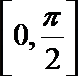
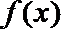
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析