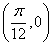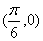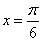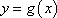- 三角函数的图象与性质
- 共712题
某同学用“五点法”画函数
时,列表并填入了部分数据,如下表:
18.请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数
析式;
19.将




正确答案
(Ⅰ)根据表中已知数据,解得
且函数表达式为
解析
(Ⅰ)根据表中已知数据可得:



且函数表达式为
考查方向
解题思路
(Ⅰ)根据已知表格中的数据可得方程组

易错点
出现粗心的错误。
正确答案
离原点

解析
由(Ⅰ)知












考查方向
解题思路
由(Ⅰ)并结合函数图像平移的性质可得,函数

易错点
平移出错。
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知复数
(1)求
(2)设





正确答案
(1)
解析
(1)∵
∴

∴当


(2)∵
∴
∴
将函数

把函数


∴
知识点
函数

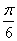
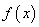
正确答案
解析
略
知识点
为了得到函数

正确答案
解析

而
由
故只需将

知识点
已知函数



正确答案
解析
由题意知,







知识点
将函数

正确答案
解析
略。
知识点
将函数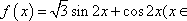
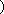
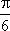
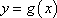
正确答案
解析
略
知识点
17.某同学用“五点法”画函数
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数
(2)将





正确答案
(1)根据表中已知数据,解得
且函数表达式为
(2)由(1)知 

因为


令


由于函数


解得





解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析