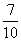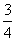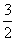- 函数的基本性质
- 共1843题
若

正确答案
解析
略
知识点
已知函数

(1)已知



(2)若






(3)记






正确答案
见解析。
解析
(1)当

其中事件

故

(2)


∴

① 当





② 当





综上,知
(3)当
当

又
而






知识点
定义在







正确答案
0
解析
略
知识点
已知函数
(1)求f(x)的最小正周期;
(2)求
(3)设

正确答案
见解析。
解析
(1)f(x)的最小正周期为T=
(2)将x=





(3)由f(3α+






∴tanα=﹣
∵cosα≠0,
则原式=


知识点
(1)已知






(2)求函数

正确答案
见解析
解析
(1)作差比较:


所以,

当
(2)解法1:
当


解法2:


设


因为
当且仅当











知识点
已知函数
(1)若f(x)=f1(x)+f2(x)﹣bf2(﹣x),是否存在a,b∈R,y=f(x)为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
(2)若a=2,b=1.求函数g(x)=f1(x)+f2(x)在R上的单调区间;
(3)对于给定的实数∃x0∈[0,1],对∀x∈[0,1],有|f1(x)﹣f2(x0)|<1成立,求a的取值范围。
正确答案
见解析。
解析
解:(1)存在a=0,b=﹣1使y=f(x)为偶函数
证明如下:此时:f(x)=e|x|+e﹣x+ex,x∈R
∴f(﹣x)=e|﹣x|+ex+e﹣x=f(x),
∴y=f(x)为偶函数,
(注:a=0,b=0)也可以)
(2)∵g(x)=e|x﹣2|+ex=
①当x≥2时g(x)=ex﹣2+ex,∴g′(x)=ex﹣2+ex>0,
∴y=g(x)在[2,+∞)上为增函数,
②当x<2时g(x)=e2﹣x+ex,
则g′(x)=﹣e2﹣x+ex,令g′(x)=0得到x=1,
(ⅰ)当x<1时g′(x)<0,
∴y=g(x)在(﹣∞,1)上为减函数。
(ⅱ) 当1≤x<2时g′(x)>0,
∴y=g(x)在(1,2)上为增函数,
综上所述:y=g(x)的增区间为[1,+∞),减区间为(﹣∞,1),
(3)∵|f1(x)﹣f2(x0)|<1,
∴f2(x0)﹣1<f1(x)<f2(x0)+1
∴∃x0∈[0,1]对∀x∈[0,1],f2(x0)﹣1<f1(x)<f2(x0)+1成立。
即:
①当b≥0时,f2(x)为增函数或常数函数,
∴当x∈[0,1]时,
∵
∴f2(x)min﹣1=f2(0)﹣1=0<f1(x)min恒成立。


∴eb+1>e1﹣a
∴a>1﹣ln(eb+1)
∵
∴
∴
∴eb+1>ea
∴a<ln(eb+1)
∵
∴
综上所述:a∈(1﹣ln(eb+1),ln(eb+1))
②当b<0时,f2(x)在[0,1]上为减函数,
∴
∵
∴f2(x)min﹣1<f1(x)min恒成立。
∴
∴a>1﹣ln2
∴


∴2>ea
∴a<ln2
∴
综上所述:∴a∈(1﹣ln2,ln2)
由①②得当b≥0时,a∈(1﹣ln(eb+1),ln(eb+1));
当b<0时,a∈(1﹣ln2,ln2)。
知识点
定义函数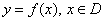
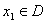
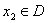
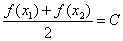
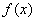
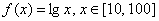
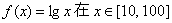
正确答案
解析
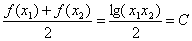
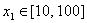
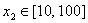
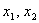
令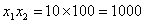
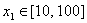
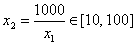
由此得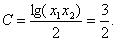
知识点
对于任意


正确答案
解析
略
知识点
已知函数


(1)若

(2)若对任意




(3)在第(2)问求出的实数






正确答案
见解析
解析
解:(1)当


由





(2)易知
依题意知

因为



(3)解法一:易知

显然

①当


令

此时


②当


令

此时




由于



解法二:对任意



由(2)可知实数
故

①当


∴
要使
若

若

解得
故

②当




要使

解得
或

综上所述,当


知识点
已知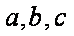
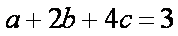
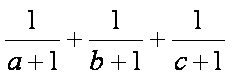
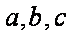
正确答案
见解析。
解析
因为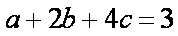
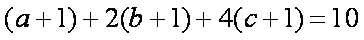
因为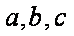
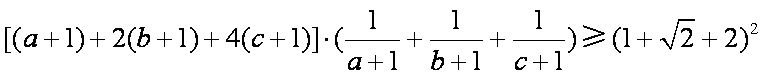
当且仅当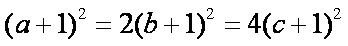
所以
所以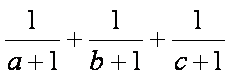
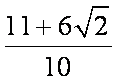
此时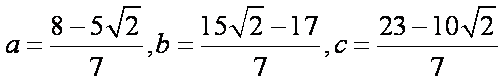
知识点
扫码查看完整答案与解析