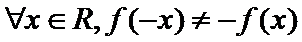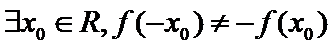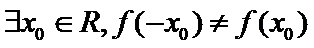- 函数的基本性质
- 共1843题
12.已知函数





正确答案
解析
B
由


而

∴对于每一组对称点

∴
考查方向
解题思路
根据已知条件判断出函数的对称中心,再利用对称性即可求出
易错点
不能由
知识点
10.设



正确答案
4
解析
由题意得:






考查方向
解题思路
反函数与原函数的对应关系是解决问题的关键,一般有两个处理方法,一是从原函数出发求其反函数,再求函数最大值,本题求反函数教困难;二是利用反函数定义域对应原函数值域,反函数值域对应原函数定义域,反函数与原函数对偶区间上单调性一致,求出函数最大值.
易错点
求f(x)
知识点
14.设函数






正确答案
解析
根据条件知P, Q的横坐标互为相反数,不妨设P(-t, t3+t2), B(t, f(t)(t>0)
若t<e,则f(t)=-t3+t2,
由∠POQ是直角得
即t4-t2+1=0.此时无解;
若t≥1,则f(t)=alnx,.由于PQ的中点在y轴上,且∠POQ是直角,
所以Q点不可能在x轴上,即t≠1.
同理
整理后得 实数a的取值范围是
考查方向
解题思路
利用垂直的条件即数量积为0是本题破题的关键,同时对变量进行分类讨论,转化为求函数的值域问题。
易错点
1、

2、分类讨论的标准,如何不重复、不遗漏。
知识点
4.若

正确答案
解析
考查方向
解题思路
利用基本不等式的性质、转化思想;综合法;不等式.即可得出
易错点
容易出现a,b相等的条件,选择答案D。
知识点
设函数
27.若

28.若

29.设

注:
正确答案
见解析
解析
考查方向
解题思路
借助导函数的正负直接求出单调区间
易错点
本题易错在第二问中的信息转化:函数

正确答案
见解析
解析
考查方向
解题思路
根据





易错点
本题易错在第二问中的信息转化:函数

正确答案
见解析
解析
考查方向
解题思路
本题解题思路
借助第二问的结论
易错点
本题易错在第二问中的信息转化:函数

20.已知

(1)讨论函数
(2)若函数

①求实数
②求证:
正确答案
见解析
解析
(1)


①当


②当




所以


(2)①由(I)知,当


当







所以

此时,

令

所以


所以
②证法一:
下面证明:当

设





即当






②证法二:
令
则:
所以函数



于是
又

考查方向
解题思路
1利用导数求函数单调性,2根据函数的零点求参数的取值范围
3构造函数求两个零点和的范围
易错点
本题必须注意函数的定义域,以及对参数进行讨论,否则求解错误。
知识点
4.下列函数中,既是偶函数,又在
正确答案
解析
由函数的奇偶性及单调性的性质可知,B和D选项为偶函数,又知,D选项在
考查方向
解题思路
根据函数单调性及奇偶性的性质,逐个选项判断
易错点
函数单调性判断错误,函数奇偶性判断错误
知识点
6.下列函数既是奇函数,又在区间
正确答案
解析















考查方向
解题思路
1.分别判断四个选项函数的奇偶性2.分别判断满足奇函数性质的函数的单调性.
易错点
本题学生们对一些复合函数的性质判断上容易出现错误.
知识点
10.已知





正确答案
解析
设

所以
考查方向
解题思路
1.先将函数


易错点
1.不知道将函数

知识点
3.设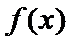
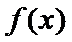
正确答案
考查方向
解题思路
1.先根据奇函数的定义得到题中命题的逆否命题;
易错点
1.全称命题的否定形式写错;2.不能正确理解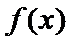
知识点
扫码查看完整答案与解析