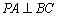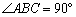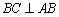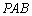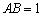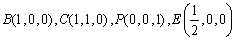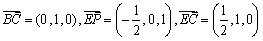- 函数的基本性质
- 共1843题
已知函数f(x)=4|a|x﹣2a+1.若命题:“∃x0∈(0,1),使f(x0)=0”是真命题,则实数a的取值范围为 。
正确答案
解析
:由:“∃x0∈(0,1),使f(x0)=0”是真命题,得:
f(0)•f(1)<0⇒(1﹣2a)(4|a|﹣2a+1)<0

⇒
故答案为:
知识点
函数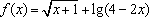
正确答案
解析
略
知识点
如果











正确答案
解析
略
知识点
设函数
(1)当


(2)设



正确答案
(1)
解析
(1)
画图正确.…………………………………………………………………………4分
当


当



所以函数的零点为
(2)由

当

当




∴
当


则



∴ 
综合 
知识点
已知数列


(1)求




(2)设



正确答案
见解析。
解析
(1)经计算



当



当



因此,数列

(2)


①、②两式相减,
得


知识点
已知函数



正确答案
6
解析
略
知识点
如图,给定两个平面向量




正确答案
解析
略
知识点
某单位员工按年龄分为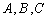
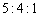
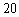
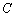
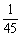
正确答案
解析
设员工总数为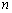
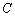
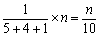
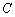
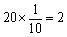
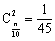
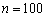
知识点
设函数





正确答案
解析
由题设

知识点
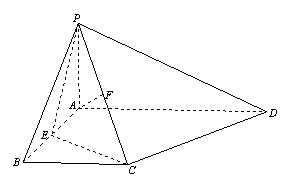
如图,在四棱锥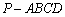
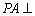
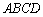
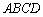
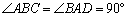
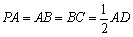
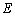
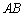
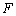
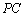
(1)求证: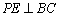
(2)求二面角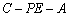
(3)若四棱锥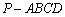
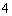
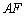
正确答案
见解析
解析
(1)∵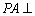
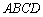
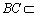
∴
∵
∴
∴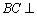
又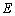
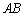
∴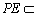
∴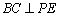
(2)建立直角坐标系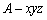
则
∴
由(1)知,
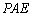
∴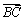
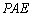
设平面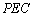
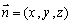
则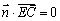
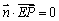
∴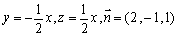
∴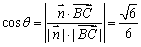
二面角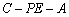
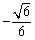
(3)连结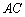
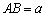
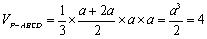
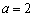
∵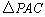
∴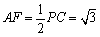
知识点
扫码查看完整答案与解析