- 极坐标刻画点的位置
- 共24题
在极坐标系中,曲线




正确答案
2
解析
略
知识点
在极坐标系中,已知圆






正确答案
见解析。
解析
由题意知,圆

设弦


因为点



又点


所以弦

知识点
在极坐标系中,求点M 

正确答案
见解析。
解析
在直角坐标系中,点M(
可得点M关于直线的对称点N的直角坐标为(1,
∴线段MN的长为 


知识点
在极坐标系中,求曲线r=2cosθ关于直线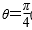
正确答案
见解析。
解析
解法一:以极点为坐标原点,极轴为x轴建立直角坐标系,
则曲线=2cosθ的直角坐标方程为 (x-1)2+y2=1,且圆心C为(1,0)。
直线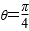
因为圆心C(1,0)关于y=x的对称点为(0,1),
所以圆心C关于y=x的对称曲线为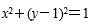
所以曲线=2cosθ关于直线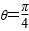
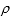
解法二:设曲线=2cosθ上任意一点为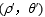
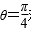
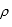
则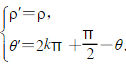
将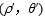
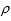
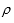
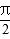
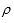
所以曲线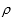
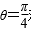
知识点
在极坐标系中,已知点P为圆ρ2+2ρsinθ﹣7=0上任一点,求点P到直线ρcosθ+ρsinθ﹣7=0的距离的最小值与最大值。
正确答案
见解析
解析
解:圆ρ2+2ρsinθ﹣7=0的普通方程为 x2+y2+2y﹣7=0,
直线ρcosθ+ρsinθ﹣7=0的普通方程为x+y﹣7=0,
设点P(2

则点P到直线x+y﹣7=0的距离
d=
所以dmin=
dmax=
知识点
扫码查看完整答案与解析
