- 函数单调性的判断与证明
- 共142题
新晨投资公司拟投资开发某项新产品,市场评估能获得




(1)设奖励方案的函数模型为

(2)下面是公司预设的两个奖励方案的函数模型:
①
试分别分析这两个函数模型是否符合公司要求.
正确答案
见解析。
解析
(1)由题意知,公司对奖励方案的函数模型
当
①


(2)①对于函数模型


则
而若使函数




②对于函数模型
当


∴
设

当



从而
∴


故该函数模型符合公司要求, ……12分
知识点
设函数
(1)当

(2)令




(3)当



正确答案
见解析。
解析
(1)依题意,

当


由 










所以

(2)


∴


所以 当


(3)因为方程

设











若
所以当

知识点
已知函数


正确答案
解析
:如图,在同一坐标系中分别作出
的图象,解析:如图,在同一坐标系中分别作出
的图象,其中a表示直线在y轴上截距,由图可知,当
直线

知识点
设




则
正确答案
解析
略
知识点
已知函数
(1)求函数
(2)设函数



正确答案
见解析。
解析
(1)







所以


(2)
所以

所以



所以
知识点
下列函数中,在
正确答案
解析
略
知识点
年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”。
(1)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?
(2)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率。
正确答案
(1)
(2)
解析
(1)该小区80岁以下老龄人生活能够自理的频率为

(2)该小区健康指数大于0的老龄人共有280人,健康指数不大于0的老龄人共有70人,所以被抽取的5位老龄人中有4位健康指数大于0,有1位健康指数不大于0.设被抽取的4位健康指数大于0的老龄人为A1,A2,A3,A4,健康指数不大于0的老龄人为B.
从这五人中抽取3人,结果有10种:
(A1,A2,A3),( A1,A2, A4), (A1,A3,A4),( A2,A3,A4),( A1,A2,B),( A1,A3,B,),( A1,A4 ,B), ( A2,A3 ,B ), ( A2,A4 ,B) , ( A3,A4 ,B)
其中恰有一位老龄人健康指数不大于0的有6种:
( A1,A2,B),( A1,A3,B,),( A1,A4 ,B), ( A2,A3 ,B ), ( A2,A4 ,B) , ( A3,A4 ,B)
所以被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率为
-----------------13分
知识点
如果对定义在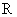
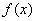
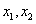
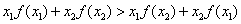
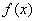
下列函数①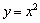
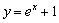
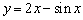
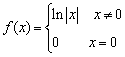
函数是“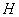
正确答案
②③
解析
略
知识点
已知函数
(1)当

(2) 若函数


正确答案
见解析。
解析
(1)解:
因为


所以

(2)当

由

当

①当




②当





③当






综上,
知识点
已知函数
(1)求函数
(2)求函数

正确答案
(1)
(2)
解析
(1)

(2)








知识点
扫码查看完整答案与解析


































