- 函数单调性的判断与证明
- 共142题
已知函数
A
B
C
D
正确答案
解析
略
知识点
已知函数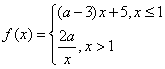
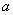
A
B
C
D
正确答案
解析
略
知识点
如图，已知△ABC中，|AC|=1，∠ABC=
（1）求
（2）求
正确答案
见解析。
解析
（1）由正弦定理，得
（2）由
∴
知识点
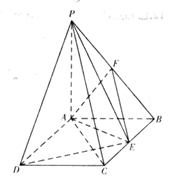
如图，PA⊥平面ABCD，ABCD是矩形，PA＝AB＝1，AD＝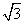
（1）求三棱锥E—PAD的体积；
（2）当点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（3）证明：无论点E在边BC的何处，都有PE⊥AF。
正确答案
见解析。
解析
（1）解 ：∵PA⊥平面ABCD，ABCD为矩形，
＝
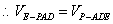
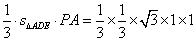
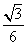
（2）当E为BC中点时，∵F为PB的中点，
∴EF∥PC ┉┉┉┉┉┉┉┉5分
∵EF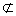
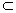
∴EF∥平面PAC，即EF与平面PAC平行。┉┉┉┉┉┉┉┉8分
(3)∵PA＝AB，F为PB的中点，
∴AF⊥PB ┉┉┉┉┉┉┉┉9分
∵PA⊥平面ABCD， ∴PA⊥BC
又BC⊥AB， ∴BC⊥平面PAB
又AF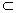
∴BC⊥AF。 ┉┉┉┉┉┉┉┉10分
又PB∩BC=B， ∴AF⊥平面PBC ┉┉┉┉┉┉┉┉11分
因无论点E在边BC的何处，都有PE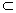
∴AF⊥PE。 ┉┉┉┉┉┉┉┉12分
知识点
已知
A
B
C
D
正确答案
解析
略
知识点
扫码查看完整答案与解析