- 函数单调性的判断与证明
- 共142题
下列函数中既是奇函数,又在(0,+∞)上单调递增的是( )
正确答案
解析
解:由于函数y=x2是偶函数,故不满足条件。
由于函数y=x3是奇函数,且在(0,+∞)上单调递增,故满足条件。
由于函数y=﹣x是奇函数,但在(0,+∞)上单调递减,故不满足条件。
由于函数 y=tanx是奇函数,故不满足条件。
故选B。
知识点
在平面直角坐标系xOy中,“直线


“ ”。
正确答案
解析
易得


知识点
设函数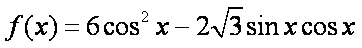
(1)求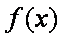
(2)在锐角△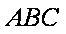
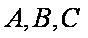
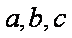
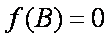
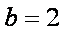
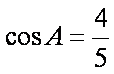
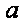
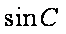
正确答案
见解析。
解析
(1)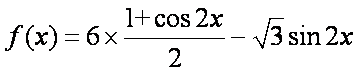
=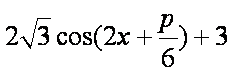
所以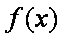
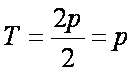
值域为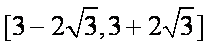
(2)由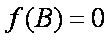
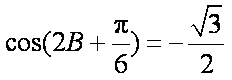
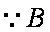
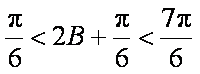
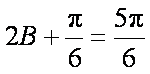
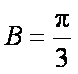
∵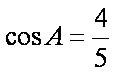
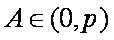
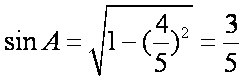
在△ABC中,由正弦定理得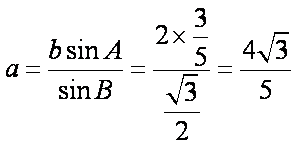
∴
知识点
“

正确答案
解析




知识点
设

数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=
(1)若k=0,求证:数列{an}是等比数列;
(2)试确定所有的自然数k,使得数列{an}能成等差数列。
正确答案
见解析
解析
(1)若


当


当


①

若



故数列

(2)(ⅰ)若
(ⅱ)若

当

当


③-④得 
要使数列{an}是公差为d(d为常数)的等差数列,必须有
而


故当



(ⅲ) 若

当


⑤-⑥得 
要使数列



且
考虑到a1=1,所以
故当

此时
(ⅳ)当







综上得,当且仅当


知识点
扫码查看完整答案与解析