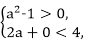- 其它不等式的解法
- 共267题
9.已知三个正实数a,b,c满足b<a+c≤2b,a<b+c≤2a,则
正确答案
解析
依题意可得
令





知识点
11.若实数x,y满足不等式组
正确答案
解析

如图,由
知识点
8.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知实数x、y满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.若

(1) 求
(2)若不等式


正确答案
(1) ∵
∴ 
∴ a = 2或a = 1(舍)
又 ∵
∴ 
∴ 
∴ 当

(2)由
∴
∴
∴ 
由
∴
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
1.已知实数系方程x2+(m+1)x+m+n+1=0的两个实根分别为x1,x2,且0<x1<1,x2>1,则
正确答案
解析
令f(x)=x2+(m+1)x+m+n+1,
则f(x)=0的两根分别满足0<x1<1,x2>1,
即有
所以
如图,
从而得到
知识点
4.已知圆面C:(x-a)2+y2≤a2-1的面积为S,平面区域D:2x+y≤4与圆面C的公共区域的面积大于
正确答案
解析
依题意并结合图形(图略)分析可知,
圆面C:(x-a)2+y2≤a2-1的圆心(a,0)应在不等式2x+y≤4表示的平面区域内,
则有
由此解得a<-1或1<a<2.
因此实数a的取值范围是(-∞,-1)∪(1,2).
知识点
13.若实数x,y满足

正确答案
2
解析
可行域如图所示,易知当直线

考查方向
解题思路
1、根据线性约束条件画出可行域。
2、画出直线
易错点
本题往往会因为不能准确地画出可行域而导致错误。
知识点
13. 过平面区域






正确答案
解析
可行域如图所示,要使

考查方向
解题思路
由不等式组画出对应的可行域,而
易错点
作出可行域,还有对
知识点
15.定义在[-2,2]上的偶函数f(x)在[-2,0]上为增,若满足f(1-m) <f(m),则m的取值范围是 .
正确答案
解析
由题设可知函数函数f(x)在[0,2]上为减函数,由图像可知离对称轴越近函数值越大,再结合函数的定义域可得
考查方向
本题主要考查了函数的性质(奇偶性和单调性)求解不等式;属于高考热点问题,常考的有函数的性质、用图(数形结合思想)、复合方程问题等。
解题思路
本题考查利用函数的单调性求解不等式,解题步骤如下:
1、由函数的性质可知函数f(x)在[0,2]上为减函数。
2、由f(1-m) <f(m)关系结合性质得到关于m的不等关系式。
易错点
本题易忽略函数的定义导致范围出错。
知识点
扫码查看完整答案与解析