其它不等式的解法_章节学习

1

题型：填空题

|

填空题 · 5 分

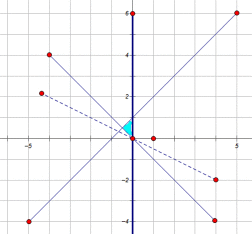
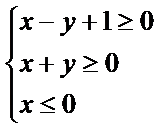
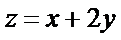
13．若实数x，y满足，则的最大值是__________。

正确答案

2

解析

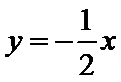
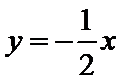
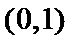
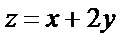
试题分析：如下图所示，画出可行域，作出直线，平移该直线，由图可知当直线经过点时，目标函数取得最大值，最大值为2，故本题答案为2

考查方向

本题主要考查线性规划问题．

解题思路

画出可行域，作出直线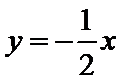，平移该直线，由图可求出目标函数的最值。

易错点

不能准确画出可行域导致出错。

知识点

其它不等式的解法

1

题型：单选题

|

单选题 · 5 分

9．不等式组表示的点集记为M，不等式组表示的点集记为N，在M中任取一点P，则P∈N的概率为（）

A

B

C

D

正确答案

D

解析

如图所示，作出不等组的可行域，根据几何概型的定义，可知红色区域面积与四边形ABCD的面积的比就是所求概率。红色区域面积不好求，由于是选择题，可以根据选项求得，容易得到，红色区域的面积比四边形面积的一半少，比四分之一多，所以结合选项，选择D

考查方向

几何概型的定义及计算

解题思路

分别求出两个不等式组所表示的区域的面积，然后利用集合概型相关性质计算求得

易错点

区域求面积，不等式取值区间

知识点

其它不等式的解法与面积、体积有关的几何概型

1

题型：简答题

|

简答题 · 12 分

21. 已知函数 .

（Ⅰ）设函数，求函数的单调区间；

（Ⅱ）若不等式≤在区间[1，e]（e=2.71828…）的解集为非空集合，求实数的取值范围

正确答案

见解析

解析

(Ⅱ) ,定义域为（0，+∞），

①当即时，令，

令，得故在上单调递减，在上单调递增

②当即时，恒成立，在（0，+∞）上单调递增。

综上，当时，的单调递减区间为，单调递增区间为。

当时，的单调递增区间为（0，+∞），无单调递减区间。

（Ⅱ）由题意可知，不等式≤在区间[1，e]（e=2.71828…）的解集为非空集合，

即在[1，e]存在使得成立，

由（Ⅰ）中，则在[1，e]存在使得

即函数在[1，e]上的最小值

由（Ⅰ）知，当时，在[1，e]上单调递增，

当时

①当即时，在[1，e]上单调递减，

②当即时，在[1，e]上单调递增，

,无解

③当即时，在上单调递减，在上单调递增此时，不合题意。

综上可得，实数的取值范围是或

考查方向

函数的单调性；导数与函数的单调性的关系；函数的最大值与最小值

解题思路

确定函数的定义域，利用导数求函数的单调区间，根据题意构造出恰当的不等式，进而求出参数的取值范围。

易错点

求导错误，构造函数不成功。

知识点

函数的单调性及单调区间导数的运算其它不等式的解法

1

题型：单选题

|

单选题 · 5 分

12．已知函数,若对任意，，则（）

A

B.

C

D

正确答案

A

解析

由题意得，函数在f(x)在x=1处取到最小值。

，所以，令求解方程，得到

，，所以当a>0时，函数得而单调递减区间是，单调递增区间是，于是可知，是函数的唯一极小值点，故，整理得，即

令，求导并令导函数为零，，得到，当

时，，函数单调递增，当时，，函数单调递减，因为，故，所以

即，所以选A。

考查方向

函数的单调性与导数的关系、函数的最值与导数的关系、不等式的定义与性质

解题思路

先判断函数的单调性，然后求导求最值。

易错点

函数单调性判断错误、求导错误

知识点

函数单调性的性质导数的运算其它不等式的解法

1

题型：单选题

|

单选题 · 5 分

9.设为坐标原点，，若满足，则的最大值为

A10

B8

C6

D4

正确答案

C

解析

1.先画出可行域，将表示成的形式，然后设，将其平移到点时，最大为6。故选C

考查方向

本题主要考查线性规划的知识，考查向量的数量积的坐标表示

解题思路

1.先画出可行域，

2.将表示成的形式，然后设，将其平移到点时，最大为6.

易错点

1.无法将正确表示出来，

2.可行域画错，导致结果出错。

知识点

平面向量数量积的运算其它不等式的解法

1

题型：填空题

|

填空题 · 5 分

12.若实数x,y满足不等式组，则的最大值是　　．

正确答案

19

解析

由题可知，求出阴影区域的三个端点坐标，分别代入目标函数计算，即可求出最大值19.

考查方向

本题主要考查线性规划

解题思路

1、表示平面区域；2、求出区域的端点坐标，即可得到结果。

易错点

本题易在表示平面区域时发生错误。

知识点

其它不等式的解法

1

题型：单选题

|

单选题 · 5 分

6.若满足且的最大值为4，则的值为（）

A

B

C

D

正确答案

A

解析

直线过定点（0,3）。将斜率进行分类讨论，

（1）当时，如图1，

画出可行区域，目标函数在点（0,3）处取得最大值3，不满足题意；

（2）当时，如图2，

画出可行区域，目标函数在直线与轴的交点处取得最值4，所以得到，将点（2,0）代入直线方程得到；

（3）当时，画出可行区域，可以得到目标函数没有最大值。

考查方向

本题主要考查线性规划问题，难度中档，属高考热点之一。常常会考查几种不同类型的目标函数的最值问题，也可以和本题一样，知道最值，求某一个参数的值或范围。

解题思路

画出三条直线，找出可行区域，再根据目标函数的斜率,对参数进行分类讨论，看哪种情形能够使得目标函数的最大值为4，找出取最大值的点，然后求出点的坐标，进而求出值

易错点

对最后一条不确定的直线，没有找到它所过的一个定点（0,3）导致不能画出大致的可行区域，而不能求出值

知识点

其它不等式的解法

1

题型：填空题

|

填空题 · 5 分

12．由不等式组确定的平面区域为A，曲线xy=1和直线y=x以及直线围成的封闭区域为B ,在A中随机取一点，则该点恰好在B内的概率为___________．

正确答案

解析

做出区域A和B的位置，如下图，B为图中绿色部分，易得，A的面积为9,求B的面积应用积分，，所以所求概率为

考查方向

几何概型，积分求面积

解题思路

根据题意做出图形，然后求出区域A和区域B的面积，进而求出概率

易错点

求不出区域B的面积

知识点

其它不等式的解法与面积、体积有关的几何概型

1

题型：单选题

|

单选题 · 5 分

4．若满足约束条件，则的最小值为（）

A

B

C

D

正确答案

C

解析

如右图，不等式组表示的可行区域为,当直线过点A时，在轴上截距的最大，求出A点坐标（0,2），代入目标函数，得到

考查方向

本题主要考察了直线的方程和线性规划中的作图能力，以及目标函数的几何意义，难度中等，属高考高频考点

解题思路

先画出不等式表示的可行区域，然后将目标函数变形成，表示斜率为1的直线过可行区域上一点，在轴上截距的最大值

易错点

1、对不等式表示的是直线的哪边部分认识不清

2、对目标函数的几何意义不了解

知识点

其它不等式的解法

1

题型：单选题

|

单选题 · 3 分

7.若x，y满足不等式组则的最大值是

A

B1

C2

D3

正确答案

C

解析

画出线性区域，区域是三角形ABC内部包括边界，其中A（1，2），B（3，2）C（2，3），设原点为O，所以OA的斜率最大为2，故选A。

考查方向

本题考查了线性规划问题，目标函数可看作线性区域内的点与原点连线的斜率。

解题思路

先画出线性区域，然后再求区域内的点与原点连线的斜率的最大值。

易错点

目标函数没能转化为斜率。

知识点

其它不等式的解法

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点