分组转化法求和
共45题

· 分组转化法求和

分组转化法求和
共45题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知各项均不相等的等差数列的前5项和，又成等比数列。

（1）求数列的通项公式；

（2）设为数列的前项和，问是否存在常数，使，若存在，求的值；若不存在，说明理由。

正确答案

见解析。

解析

（1）设数列的公差为，由已知得，

又成等比数列，所以

解得：

所以

（2）

所以

故存在常数

知识点

分组转化法求和

题型：简答题

简答题 · 12 分

已知函数，数列{}的前n项和为，点都在函数y＝f（x）的图象上。

（1）求数列{}的通项公式；

（2）令，是数列{}的前n项和，求；

（3）令

正确答案

见解析。

解析

知识点

分组转化法求和

题型：简答题

简答题 · 12 分

已知等比数列成等差数列。

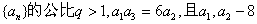
（1）求数列{an}的通项公式；

（2）设

正确答案

见解析。

解析

知识点

分组转化法求和

题型：简答题

简答题 · 12 分

已知点（1,2）是函数的图象上一点，数列的前n项和.

（1）求数列的通项公式；

（2）将数列前2013项中的第3项，第6项，…，第3k项删去，求数列前2013项中剩余项的和.

正确答案

见解析。

解析

（1）把点（1,2）代入函数，得.……………………（1分）

…………………………………………（2分）

当时，…………………………………（3分）

当时，

……………………………………………（5分）

经验证可知时，也适合上式，

.…………………………………………………………（6分）

（2）由（1）知数列为等比数列，公比为2，故其第3项，第6项，…，第2013项也为等比数列，首项公比为其第671项………………………………………………………………（8分）

∴此数列的和为……………………（10分）

又数列的前2013项和为

…………………………………（11分）

∴所求剩余项的和为…（12分

知识点

由an与Sn的关系求通项an分组转化法求和

题型：填空题

填空题 · 5 分

对于每一个正整数，设曲线在点（1,1）处的切线与轴的交点的横坐标为，令，则= 。

正确答案

-2

解析

知识点

导数的几何意义分组转化法求和

继续学习学习下一知识点

下一知识点 : 错位相减法求和

百度题库 > 高考 > 文科数学 > 分组转化法求和

扫码查看完整答案与解析