- 分组转化法求和
- 共45题
已知数列




正确答案
解析
略
知识点
已知数列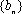
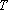
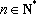
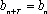
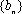
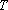
数列



数列
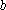

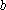
数列
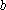


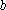

(1)对于数列②,它的一个通项公式可以是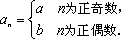
(2)求数列③的前
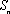
(3)在数列③中,若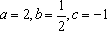
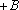
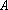
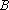

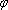
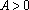
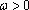
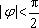
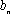
正确答案
见解析
解析
(1)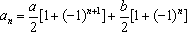
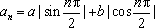
(2)当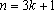
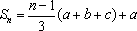
当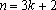
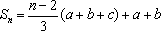
当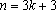
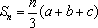
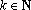
(3)由题意,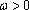
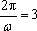
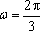
于是
把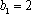
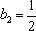
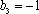
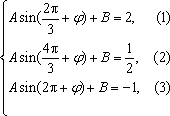
由(1)(2)可得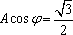
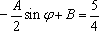
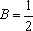
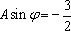
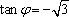
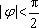
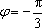
于是可求得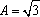
故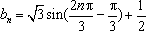
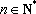
或写成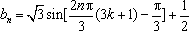
知识点
设数列
(1)求数列
(2)设



正确答案
(1)
(2)
解析
(1)设等比数列







(2) 


知识点
已知数列{an}的相邻两项an,an+1是关于x的方程x2﹣2nx+bn=0(n∈N*)的两实根,且a1=1。
(1)求证:数列
(2)设Sn是数列{an}的前n项和,求Sn;
(3)问是否存在常数λ,使得bn>λSn对∀n∈N*都成立,若存在,求出λ的取值范围,若不存在,请说明理由。
正确答案
见解析。
解析
(1)证明:∵an,an+1是关于x的方程x2﹣2n•x+bn=0(n∈N*)的两实根,
∴
∵
故数列

(2)由(1)得
即


(3)由(2)得
要使bn>λSn,对∀n∈N*都成立,
即
①当n为正奇数时,由(*)式得:
即
∵2n+1﹣1>0,∴
故
∴λ<1。
②当n为正偶数时,由(*)式得:
∵2n﹣1>0,∴
故

∴
知识点
数列


(1)求数列
(2)若数列




正确答案
见解析
解析
解析:(1)当

当


(2)当
当

则
知识点
扫码查看完整答案与解析