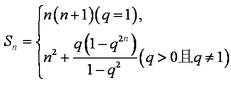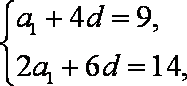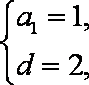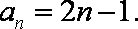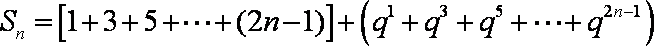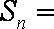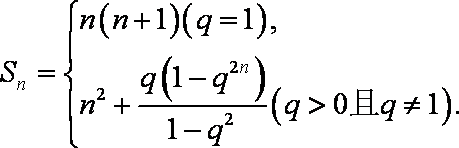- 分组转化法求和
- 共45题
1
题型:简答题
|
已知等差数列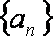

(1)求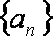
(2)若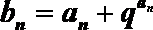
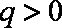
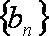
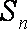
正确答案
(1)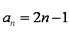
解析
解析:(1)设
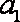
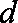
由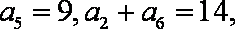
解得
所以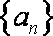
(2)由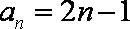
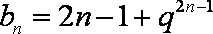
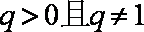
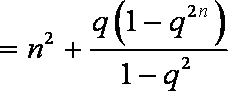
② 当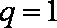
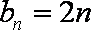
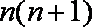
所以数列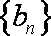
知识点
由数列的前几项求通项等差数列的基本运算分组转化法求和
1
题型:填空题
|
12.已知数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
分组转化法求和
1
题型:填空题
|
15.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f″(x)是函数y=f(x)的导数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点为函数y=f(x)的“拐点”。有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,求:
(1)函数f(x)=x3-3x2+3x对称中心为___________;
(2)若函数

正确答案
(1,1) ; 2010
解析
解析已在路上飞奔,马上就到!
知识点
导数的运算利用导数求函数的极值分组转化法求和进行简单的合情推理
1
题型:填空题
|
12.已知

正确答案
2008
解析
解析已在路上飞奔,马上就到!
知识点
对数的运算性质对数函数的图像与性质分组转化法求和
1
题型:简答题
|
20.数列{an}中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)。
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn。
正确答案
解:(1)由an+2=2an+1-an
d=
(2)由an=10-2n≥0可得n≤5,当n≤5时,Sn=-n2+9n,当n>5时,Sn=n2-9n+40,故Sn=
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式分组转化法求和
下一知识点 : 错位相减法求和
扫码查看完整答案与解析