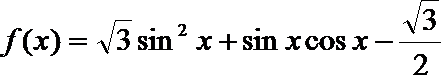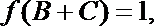- 正弦函数的对称性
- 共37题
6.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数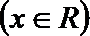
(Ⅰ)若
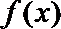
(Ⅱ)求函数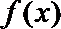
(Ⅲ)在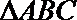
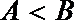
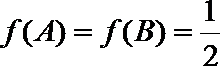
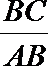
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数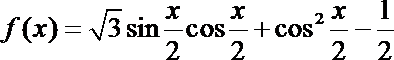
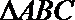
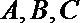
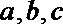
(I)求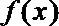
(Ⅱ)若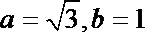
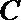
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
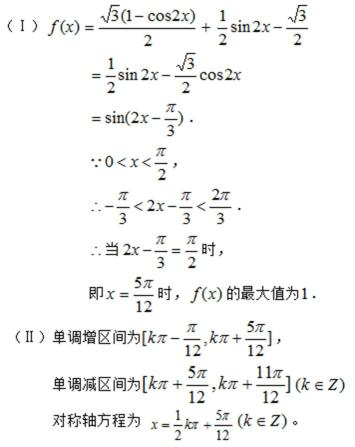
16.已知向量
(I)求函数
(II)求函数
正确答案
解: (I)
(II)∵
令

∴对称点为
由
∴对称轴方程为
∵

∴
∴

解析
解析已在路上飞奔,马上就到!
知识点
5.将函数y=sin(2x+

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数

正确答案
解析
由图可知,
故
即

又因为

所以

应选C.
考查方向
解题思路
1.结合图形算出周期;
2.利用周期与对称轴之间的距离关系,得出结果,
应选C。
易错点
本题不易理解周期与对称轴之间,以及对称轴与对称轴之间的距离关系。
知识点
9.将函数f(x)=3sin(4x+

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数


(1)求
(2)3


正确答案
(1)
(2)
解析
试题分析:本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关函数的知识,即可解决本题,解析如下:
(1)因为

所以

解
得:
所以函数
(2) 因为
由正弦定理,
得
因为

所以


所以

根据正弦函数的图象可以看出,


此时

所以
考查方向
本题考查了三角恒等变换、三角函数的图像及性质、利用正余弦定理判断三角函数的形状等知识点,属于简单题,只要掌握这些知识点,就可做对本题。
易错点
相关知识点不熟悉导致出错。
知识点
扫码查看完整答案与解析