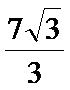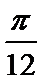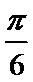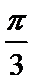- 正弦函数的对称性
- 共37题
1
题型:填空题
|
10.已知△ABC的三边长分别为3,5,7,则该三角形的外接圆半径等于____.
正确答案
解析
设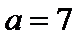
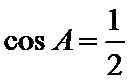
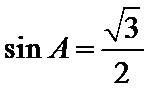
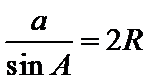
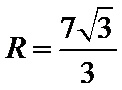
考查方向
解三角形
解题思路
利用余弦定理得余弦值,利用基本关系求正弦值,利用正弦定理求半径.
易错点
正弦定理几何意义
知识点
正弦函数的对称性
1
题型:简答题
|
△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为
17.求a和sinC的值;
18.求
第(1)小题正确答案及相关解析
正确答案
a=8,
解析
试题分析:由面积公式可得


△ABC中,由








考查方向
本题主要考查正弦定理、余弦定理等基础知识,考查基本运算求解能力.
解题思路
解三角形问题实质是附加条件的三角变换,因此在解三角形问题的处理中,正弦定理、余弦定理就起到了适时、适度转化边角的作用,分析近几年的高考试卷,有关的三角题,大部分以三角形为载体考查三角变换.
易错点
三角形面积公式的运用及边角关系的互化
第(2)小题正确答案及相关解析
正确答案

解析
试题分析:(II)直接展开求值.

考查方向
本题主要考查三角变换,考查基本运算求解能力.
解题思路
解三角形问题实质是附加条件的三角变换,分析近几年的高考试卷,有关的三角题,大部分以三角形为载体考查三角变换.
易错点
和角公式的正确运用
1
题型:
单选题
|
4.将函数f (x) =
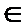
正确答案
D
解析
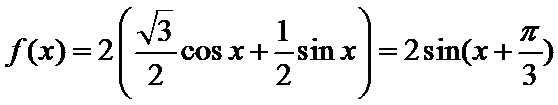
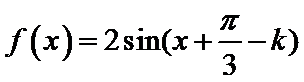
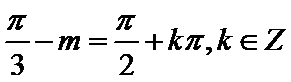
考查方向
本题主要考查了函数y=Asin(ωx+φ)的图象变换.
解题思路
先利用辅助角公式合二为一,再利用三角函数的性质找出正确答案。
易错点
三角函数的性质。
知识点
正弦函数的对称性三角函数中的恒等变换应用三角函数的最值
1
题型:
单选题
|
4.下列函数中,最小正周期为
正确答案
A
解析
由最小正周期为


考查方向
本题主要考查了求满足相应性质的解析式,在近几年的各省高考题出现的频率较高,常考的有三角恒等变形,函数单调性、周期性、对称型、奇偶性等知识点交汇命题。
解题思路
由最小正周期和关于原点对称求解出相应的解析式
易错点
本题易在对性质和三角恒等变形不到们导致出错 。
知识点
单位圆与周期性正弦函数的对称性
1
题型:填空题
|
正确答案
2
知识点
正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用
下一知识点 : 余弦函数的图象
扫码查看完整答案与解析