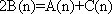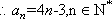- 充要条件的应用
- 共51题
1
题型:简答题
|
已知数列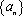
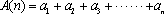
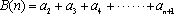
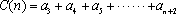
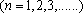
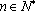
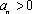
(1)若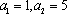
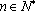
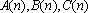
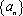
(2)证明:数列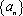
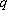
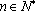
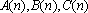
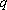
正确答案
见解析
解析
解析:(1)
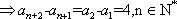
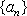
(2)(必
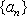
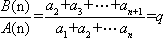
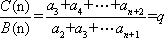
(充分性):若对于任意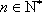
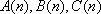
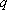
则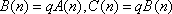
于是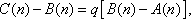
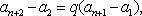
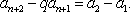
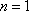
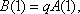
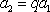
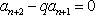
因为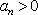
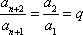

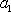
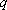
综上,数列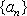
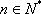

知识点
充要条件的应用等差数列的性质及应用等比数列的判断与证明等比数列的性质及应用
1
题型:
单选题
|
若命题
正确答案
D
解析
知识点
充要条件的应用
1
题型:
单选题
|
“

正确答案
C
解析
略
知识点
充要条件的应用
1
题型:
单选题
|
“



正确答案
C
解析
若命题“









知识点
充要条件的应用
1
题型:简答题
|
17.已知




(1)若


(2)若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
充要条件的应用含有逻辑联结词命题的真假判断
下一知识点 : 命题的否定
扫码查看完整答案与解析