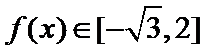三角函数的图象与性质_章节学习

1

题型：填空题

|

填空题 · 5 分

14.已知函数,,若函数在区间内单调递增,且函数的图像关于直线对称,则的值为．

正确答案

解析

由在区间内单调递增,且的图像关于直线对称,可得 ,且,所以

考查方向

本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，考查了正弦函数的图象和性质，正确确定k的值是解题的关键，属于中档题．

解题思路

本题将三角函数单调性与对称性结合在一起进行考查,叙述方式新颖,是一道考查能力的好题.注意本题解法中用到的两个结论:①的单调区间长度是半个周期;②若的图像关于直线对称,则或.

易错点

函数性质的灵活运用

知识点

正弦函数的定义域和值域

1

题型：简答题

|

简答题 · 12 分

已知．

16.求的值；

17.求的值．

第(1)小题正确答案及相关解析

正确答案

（1）；

解析

（1）

考查方向

本题考察了两角和的正切公式、特殊角的三角函数值、二倍角的正、余弦公式；同角三角函数的基本关系等，属于中等题.

解题思路

（1）由两角和的正切公式展开，代入数值，即可得的值；（2）先利用二倍角的正、余弦公式可得，再分子、分母都除以可得，代入数值，即可得的值．

易错点

注意公式的应用及计算中不要出错。

第(2)小题正确答案及相关解析

正确答案

（2）．

解析

（2）

考查方向

本题考察了两角和的正切公式、特殊角的三角函数值、二倍角的正、余弦公式；同角三角函数的基本关系等，属于中等题.

解题思路

（1）由两角和的正切公式展开，代入数值，即可得的值；（2）先利用二倍角的正、余弦公式可得，再分子、分母都除以可得，代入数值，即可得的值．

易错点

注意公式的应用及计算中不要出错。

1

题型：填空题

|

填空题 · 6 分

11. 已知，则A=______，b= ．

正确答案

；1．

解析

，所以

考查方向

本题主要考查了三角恒等变换等知识，为高考题的必考题，在近几年的各省高考题出现的频率较高

解题思路

先由题意，再求出即可

易错点

对三角函数的三角恒等变换不熟悉，计算错误

知识点

正弦函数的定义域和值域

1

题型：填空题

|

填空题 · 5 分

11.sin750°= 。

正确答案

解析

由诱导公式可得

考查方向

本题考查了三角函数诱导公式的问题

解题思路

本题也可以看作是一个来自于课本的题，直接利用课本公式解题，这告诉我们一定要立足于课本．有许多三角函数的求值问题一般都是通过三角函数的公式把函数化为特殊角的三角函数值而求解．

易错点

本题考查了三角函数诱导公式的问题，在诱导公式的应用中易错。

知识点

正弦函数的定义域和值域

1

题型：简答题

|

简答题 · 14 分

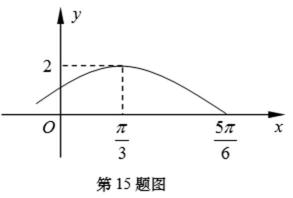
15．设函数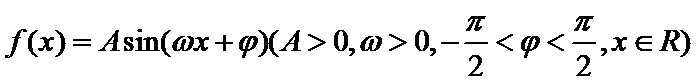的部分图象如图所示.

（1）求函数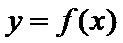的解析式；

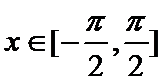
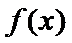
（2）当时，求的取值范围.

正确答案

（1）；

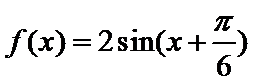
（2）

解析

试题分析：本题属于三角函数图像的基本问题，题目的难度是逐渐由易到难，（1）直接按照求A、ω、φ步骤来求（2）转化成求函数的最值，要结合图像，要特别注意函数的定义域。

（1）由图象知，，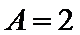

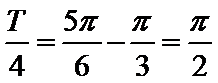
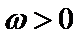
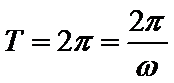
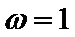
又，，所以，得.

所以，将点代入，得，

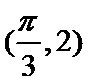
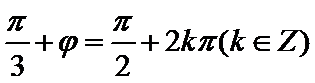
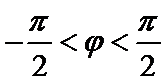
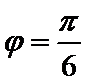
即，又，所以.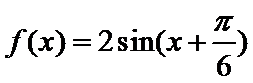

所以.

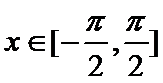
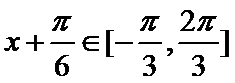
（2）当时，，

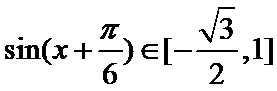
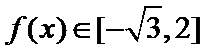
所以，即.

考查方向

本题考查了三角函数的图形和性质，利用三角函数的图像求函数解析式，根据函数的图像求函数的取值范围。

解题思路

本题考查三角函数的图形和性质，解题步骤如下：

1、根据函数图像，确定A、ω、φ，进而求出函数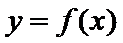的解析式。

2、求函数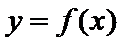的解析式，必须在给定的x的取值范围内求解。

易错点

1、第一问中的根据角的范围如何确定φ。2、第二问中求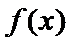的取值范围，必须先求出x的取值范围，同时结合三角函数的图像去分析。

知识点

正弦函数的定义域和值域由y=Asin（ωx+φ）的部分图象确定其解析式

1

题型：单选题

|

单选题 · 5 分

6.若，则（）

A

B

C

D

正确答案

D

解析

考查方向

本题主要考查了同角三角函数间的基本关系和二倍角等知识，为高考题的必考题，在近几年的各省高考题出现的频率较高

解题思路

求出

易错点

对同角三角函数间的基本关系和二倍角理解出现错误、计算错误

知识点

正弦函数的定义域和值域

1

题型：填空题

|

填空题 · 4 分

函数的最小正周期是。

正确答案

解析

对解析式进行降幂扩角，转化为，可知其最小正周期为，本题主要考察了二倍角余弦公式的灵活运用，属容易题。

知识点

正弦函数的对称性函数y=Asin（ωx+φ）的图象变换

1

题型：简答题

|

简答题 · 12 分

在中，角所对的边分别为，且满足

（1）求角的大小；

（2）求的最大值，并求取得最大值时角的大小。

正确答案

见解析。

解析

（1）由正弦定理得sinCsinA=sinAcosC，

∵0＜A＜π，

∴sinA＞0，

∴sinC=cosC，又cosC≠0，

∴tanC=1，又C是三角形的内角

即∠C=…

（2）sinA﹣cos（B+C）=sinA﹣cos（π﹣A）

=sinA+cosA=2sin（A+）…

又0＜A＜，＜A+＜，

所以A+=即A=时，2sin（A+）取最大值2。

综上所述，sinA﹣cos（B+C）的最大值为2，此时A=，B=…

知识点

正弦函数的对称性

1

题型：简答题

|

简答题 · 13 分

设数列{}的前n项和为.若对任意的正整数n,总存在正整数m,使得，则称{}是“H数列。”

（1）若数列{}的前n项和=（n），证明：{}是“H数列”；

（2）设数列{}是等差数列，其首项=1.公差d0.若{}是“H数列”，求d的值；

（3）证明：对任意的等差数列{}，总存在两个“H数列” {}和{}，使得=（n）成立。

正确答案

见解析。

解析

（1）证明：∵= ，∴==（n），又==2= ，∴（n）。 ∴存在m=n+1使得

（2）=1+（n-1）d ，若{}是“H数列”则对任意的正整数n,总存在正整数m,使得。=1+（m-1）d成立。化简得m= +1+，且d0

又m ，，d，且为整数。

（3）证明：假设成立且设都为等差数列，则

n+=+（-1），=++1，

∴= （）同文= （）

取==k由题==+（-1）++（-1）

=（）+（n-1）（）=（n+k-1））

可得{}为等差数列。即可构造出两个等差数列{}

和{}同时也是“H数列”满足条件。

知识点

正弦函数的对称性

1

题型：填空题

|

填空题 · 4 分

若则

正确答案

解析

略

知识点

正弦函数的对称性

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点