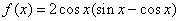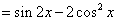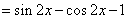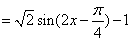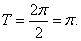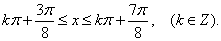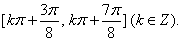- 三角函数的图象与性质
- 共601题
设函数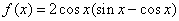
(1)求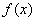
(2)求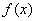
正确答案
见解析。
解析
解:(1)∵
∴函数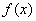
(2)∵函数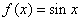
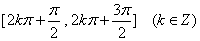
由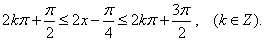
得
∴函数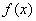
知识点
函数
正确答案
解析
略
知识点
如果函数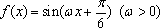

正确答案
解析
略
知识点
已知函数


(1)求

(2)当

正确答案
(1)



(2)[
解析
(1)

因为


于是
由


所以


(2)因为

则
所以


知识点
若点


正确答案
解析
略
知识点
已知函数
(1)求函数
(2)若

正确答案
见解析。
解析
(1)由

所以函数



(2)解法1:由



∴
【解法2:由

代入





∴
知识点
已知函数
(1)求

(2)求函数在区间
正确答案
(1)
(2)
解析
(1)
因为





(2)当

所以当

当

知识点
已知函数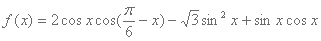
(1)求f(x)的最小正周期;
(2)将函数,y=f(x)的图象上各点的横坐标缩短到原来的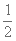
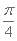
正确答案
见解析。
解析
知识点
函数
正确答案
解析
略
知识点
在△

(1)求角
(2)若



正确答案
(1)
(2)
解析
(1)解:由
所以原式化为
因为


因为

(2)解:由余弦定理,得

因为 


因为 

知识点
扫码查看完整答案与解析