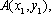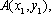- 三角函数的图象与性质
- 共601题
在正三角形





正确答案
解析
略
知识点
在△





正确答案
解析
略
知识点
在




正确答案
解析
略
知识点
已知










正确答案
解析
略
知识点
已知


正确答案
-1
解析
略
知识点
已知函数
(1)求函数
(2)求函数

正确答案
(1)
(2)
解析
(1)


周期为
(2)









知识点
已知
(1)求
(2)当

正确答案
(1)
解析
(1)
=
=
=
∴ 
(2) ∵
∴ 
当


当


∴当

知识点
已知函数
(1)求函数
(2)在




正确答案
见解析
解析
知识点
设抛物线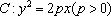
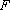
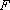
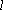
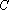
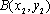
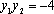
(1)求抛物线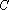
(2)若直线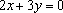
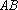
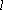
(3)若点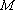

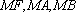
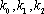
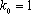
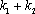

正确答案
见解析
解析
解析:(1)设直线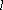
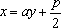
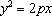
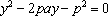
由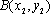
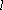
故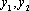
∴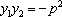
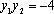
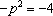
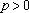
所以抛物线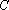
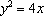
【另法提示:考虑直线l垂直于x轴这一特殊情形,或设直线l方程为点斜式】
(2)由(1)可知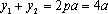
设点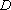
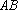
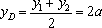
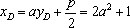
由题意知点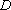
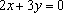
∴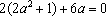
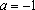
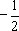
设直线

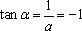
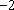
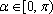
故直线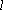
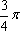
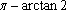
【另法提示:设直线l方程为点斜式】
(3)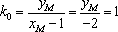
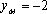
由(2)知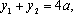
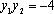
∴
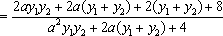
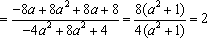
所以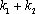
【另法提示:分直线l斜率存在与不存在两种情形讨论,斜率存在时设直线l方程为点斜式】
知识点
已知函数

如图3示,则函数

正确答案

解析
由图象易得

知识点
扫码查看完整答案与解析