三角函数的图象与性质
共601题

三角函数的图象与性质
共601题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 8 分

已知函数.

（1）求函数的最大值，并指出取得最大值时相应的的值；

（2）求函数的单调增区间。

正确答案

见解析。

解析

（1）

+1+1 ---------------------2分

(注：此处也可是+1等)

所以的最大值是3

此时，即 ----------------------------4分

（2）因为余弦函数的增区间为,

∴ --------------------------6分

∴

∴的单调增区间为 -------------------8分

知识点

正弦函数的单调性三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 12 分

已知函数.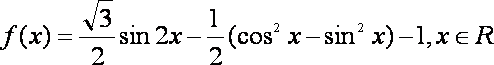

（1）求函数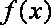的单调递增区间；

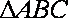
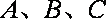
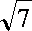
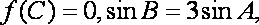
（2）设的内角的对边分别为a、b、c，若c=，求a,b的值

正确答案

见解析。

解析

（1）………………………………4分

……………………………6分

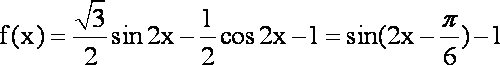
（2）由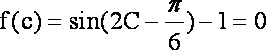得

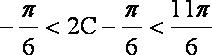
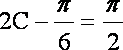
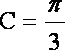
又，所以，即……………………………………8分

由余弦定理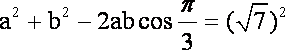①…………………………………………………10分

由得②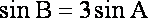

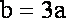
由①②得，a=1,b=3………………………………………………………………………12分

知识点

正弦函数的单调性三角函数中的恒等变换应用正弦定理余弦定理

题型：简答题

简答题 · 14 分

中，角A，B，C的对边分别是，，，

若，，且是与的等比中项。

（1）求A，B，C；

（2）若函数（）满足，求函数的解析式及单调递减区间。

正确答案

见解析。

解析

（1）根据题意得，即，解得.

∴.∴，∴.

（2）∵，，，∴，

又∵，∴，，∴.

由，可得单调递减区间为

知识点

正弦函数的单调性正弦定理余弦定理

题型：填空题

填空题 · 5 分

设△ABC的三个内角A、B、C所对的三边分别为a, b, c，若△ABC的面积为S = a2－(b－c)2，则=

正确答案

解析

易知：，又S = a2－(b－c)2= ，所以，所以=4.

知识点

正弦函数的单调性

题型：简答题

简答题 · 12 分

在中，角A、B、C的对边分别为a，b，c，三边a，b，c成等比数列。

（1）角A，B，C成等差数列，求的值；

（2）若，求。

正确答案

（1）（2）

解析

知识点

正弦函数的单调性

题型：简答题

简答题 · 12 分

已知，，函数，

（1）求方程的解集；

（2）求函数的最小正周期及其单调增区间

正确答案

见解析

解析

（1） 2分

由得即 5分

故方程＝0的解集为 6分

（2） 7分

9分

∴函数的最小周期 10分

由得

故函数的单调增区间为，（开区间也可以）12分

知识点

三角函数的化简求值三角函数的周期性及其求法正弦函数的单调性三角函数中的恒等变换应用平面向量数量积的运算

题型：简答题

简答题 · 12 分

已知向量，向量，函数.

（1）求的最小正周期；

（2）已知，，分别为内角，，的对边，为锐角，，且恰是在，上的最大值，求，和的面积。

正确答案

见解析。

解析

（1） ………2分

. …………5分

因为，所以. …………6分

（2）由（1）知：，时, ，

由正弦函数图象可知,当时取得最大值，

所以,. …………8分

由余弦定理，，∴，

∴ ， ………10分

从而. …………12分

知识点

正弦函数的单调性

题型：填空题

填空题 · 5 分

小明通过做游戏的方式来确定周末活动，他随机地往单位圆中投掷一点，若此点到圆心的距离大于，则周末看电影；若此点到圆心的距离小于，则周末打篮球；否则就在家看书，那么小明周末在家看书的概率是 ▲ 。

正确答案

解析

略

知识点

正弦函数的单调性

题型：简答题

简答题 · 12 分

已知函数。

（1）当时，求函数的单调递增区间；

（2）设△ABC的内角A,B,C的对应边分别为a,b,c，且,若向与向量共线，求a,b的值.

正确答案

见解析

解析

（1）==

令，

解得即…………4分

,f(x)的递增区间为 ………………6分

（2）由,得

而,所以,所以得

因为向量与向量共线，所以，

由正弦定理得:　　　　 ①……………10分

由余弦定理得:,即a2+b2－ab=9　②………11分

由①②解得……………12分

知识点

正弦函数的单调性三角函数中的恒等变换应用正弦定理余弦定理平面向量共线（平行）的坐标表示

题型：简答题

简答题 · 10 分

设

（1）求函数的最小正周期和单调递增区间

（2）当

正确答案

见解析。

解析

（1）……….2分

……………………………….1分

所以函数的单调递增区间是…………………………6分

（2）

…………………………………12分

知识点

三角函数的周期性及其求法正弦函数的单调性三角函数中的恒等变换应用三角函数的最值

继续学习学习下一知识点

下一知识点 : 三角恒等变换

百度题库 > 高考 > 文科数学 > 三角函数的图象与性质

扫码查看完整答案与解析