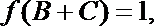- 三角函数的图象与性质
- 共601题
18.已知函数
(Ⅰ)求
(Ⅱ)设

正确答案
(Ⅰ)∵


(Ⅱ)∵









故
解析
解析已在路上飞奔,马上就到!
知识点
16. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知向量


(1)求函数
(2)当

(3)说明

正确答案
(2)由
解得
∵取k=0和1且


∴


法二:∵

∴由

解得

∴


(3)



再把所得各点的横坐标缩短到原来的
最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),
得到
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)求函数
(2)若

正确答案
(1)已知函数
∴
令
则
即函数
(2)由已知
∴ 当
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数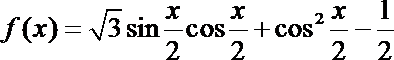
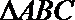
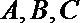
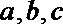
(I)求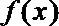
(Ⅱ)若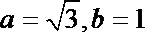
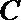
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,椭圆

(1)求椭圆C的标准方程;
(2)已知顶点在坐标原点的抛物线的焦点为椭圆的上焦点



(3)若直线


正确答案
答案:
解析
解析已在路上飞奔,马上就到!
知识点
15.三棱锥A-BCD中,BA


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数




(I)求函数
(II)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

(1)求函数
(2)若函数




正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析