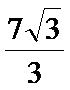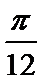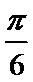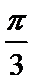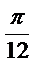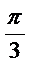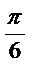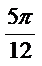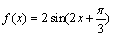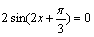- 三角函数的图象与性质
- 共601题
10.已知△ABC的三边长分别为3,5,7,则该三角形的外接圆半径等于____.
正确答案
解析
设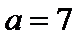
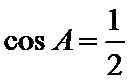
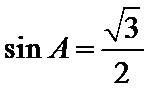
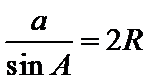
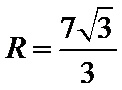
考查方向
解题思路
利用余弦定理得余弦值,利用基本关系求正弦值,利用正弦定理求半径.
易错点
正弦定理几何意义
知识点
4.将函数f (x) =
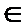
正确答案
解析
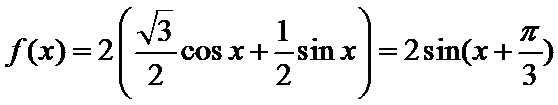
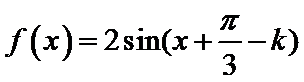
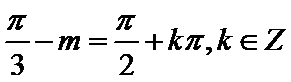
考查方向
解题思路
先利用辅助角公式合二为一,再利用三角函数的性质找出正确答案。
易错点
三角函数的性质。
知识点
4.下列函数中,最小正周期为
正确答案
解析
由最小正周期为


考查方向
解题思路
由最小正周期和关于原点对称求解出相应的解析式
易错点
本题易在对性质和三角恒等变形不到们导致出错 。
知识点
9.若将函数


正确答案
解析
由

又所得图象关于y轴对称,则
∴当k=-1时,

故选C.
考查方向
解题思路
把函数式



易错点
三角函数图象的平移应遵循“左加右减”的原则.
知识点
1.方程2sin θ=cos θ(θ∈[0,2π))的根的个数是( )
正确答案
解析
因为2sin θ>0,所以cos θ>0
令sin θ=x,-1≤x≤1,则问题转化为方程2x=
记C1:y=2x,C2:y=
则问题又转化为两条曲线在x∈[-1,1]内交点个数的问题.
在同一坐标系中画出它们的图象,如图所示
故选B.
知识点
已知函数
(1)求
(2)求函数

正确答案
(1)
(2)最大值
解析
(1)由已知,得


所以 
即 

(2)因为 

于是,当



当



知识点
11.已知曲线
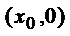


正确答案
解析
利用和差公式求出;
因为关于(x0,0)中心对称。
则,解的x=
考查方向
三角函数的性质。和差公式
解题思路
求出一种三角函数的表达式,利用中心对称必为y0=0,反求出x0
易错点
分清中心对称和轴对称
教师点评
三角函数的考察,抓住三角函数的性质进行解答
知识点
5.设











正确答案
解析
由余弦定理得:






知识点
4. 下列函数中,最小正周期为

A.
正确答案
解析
由最小正周期为2,可以排除D,对称轴为

考查方向
解题思路
利用排除法解题,从已知入手,进行排除。
易错点
熟悉三角函数
知识点
扫码查看完整答案与解析